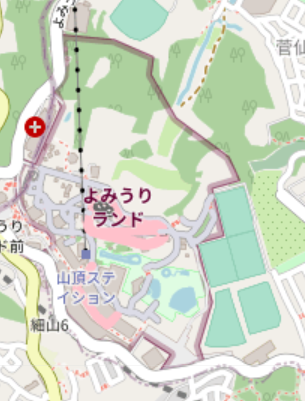
標準OSMでは、テーマパークや動物園の境界線は下に示すように、ラインの垂直方向に gradation のかかった線(色違いの二重線)を引く。
できればこれと同等のことを C# でやってみたい。

Mapnik版では次のようにしている。外側に濃くて細い線、内側に薄くて太い線を描く。 濃い、薄いは色ではなく透過率で実現している。
offsetの指定により、多角形の境界線より少し内側に線を引いている。
<Rule>
&min_zoom10;
&max_zoom13;
<Filter>([tourism] = 'theme_park' or [tourism] = 'zoo')
and [way_area] >= 100000 and not [name] is null</Filter>
<LineSymbolizer stroke="#660033" stroke-width="1" offset="-0.5" stroke-opacity="0.6"/>
<LineSymbolizer stroke="#660033" stroke-width="4" offset="-2" stroke-opacity="0.3"/>
</Rule>
C# では多重線を引く機能がある[1]。順に描画区間、空白区間、描画区間、空白区間・・・を配列で指定する。
pen.CompoundArray = new float[] {0f, 0.33f, 0.67f, 1.0f};
e.Graphics.DrawLine(pen, point1, point2);
試行錯誤の結果、C# では次のようにした。inner は alphaを下げ、普通に線を描いている。 outer は同じ太さであるが、実質外側の25%だけを描画している。alpha は上げて濃く見える ようにしている。折れ線の継ぎ目が少し目立つので、LineCap.Roundも試したが、使わない方が 良さそうだった。
foreach (OSM osm in osms) {
if (osm.type != 2) continue;
if (osm.Tourism == ValCode.theme_park || osm.Tourism == ValCode.zoo) {
Pen penOuter = new Pen(Color.FromArgb(150, 0xcc, 0x00, 0x66), 4.0f);
Pen penInner = new Pen(Color.FromArgb( 75, 0xcc, 0x00, 0x66), 4.0f);
penOuter.CompoundArray = new float[] {0, 0.01f, 0.75f, 1.0f};
//penInner.StartCap = LineCap.Round;
DrawLine(g, penOuter, zoom, X, Y, osm.points);
DrawLine(g, penInner, zoom, X, Y, osm.points);
DrawString(g, zoom,X,Y, osm.center, "Meiryo UI",
FontStyle.Bold, brThemePark, 14, 0, osm.name, penStdHalo);
}
}
描画結果を下に示す。まだ、これから描画するものがたくさんある[2021.4.25]。
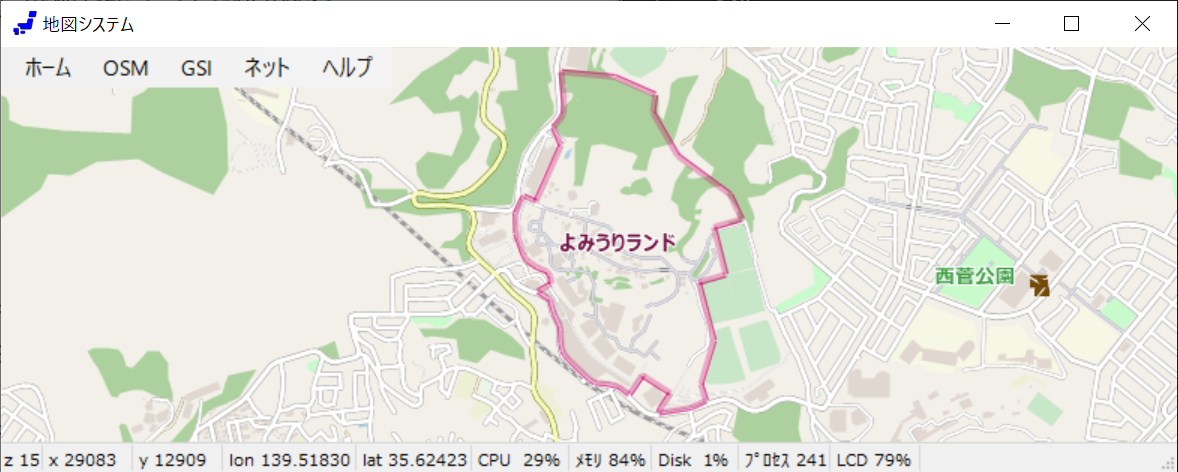
Mapnikの場合、フリー描画ソフトを使っているはずだが、その方法で交点を求めているか、 あるいはもう少し効率の良い方法があるのかも知れない。
頂点座標を単純に拡大または縮小する方法ではうまく行かない。 例えば、頂点座標が (0, 0) では移動が起きない。絶対値が大きいほど大きく移動する。線分の平行移動とはならない。
自前のプログラムで、 多角形の少し内側とか外側に境界線を引くのは面倒である。 線分ごとに平行線を描くのがスタート点となるが、線分同士が交差したり、しなかったりする。 平行線分同士の交点を算出して、そこを求める多角形の交点とすればよい。
頂点が重なっていた場合、一つのものとして扱わないと、線分にはならない。
平行な線分同士では交点は存在しないが、元々の線分は端点でつながっていたものであるから、 それぞれを平行移動した線分を無限の長さの直線とすれば、必ず交点は存在する。