トップ >
デジタル回路 > カルノー図法
カルノー図法
カルノー図
カルノー図法は、表を使って、論理式を簡単化する。
例として論理式
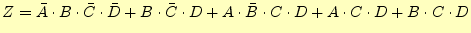
(1)
を簡単化する。
(参考:http://akita-nct.jp/yamamoto/lecture/2003/2E/ karnaugh_diagram/node3.html)
カルノー図のための表をまず作成する。
論理変数が4個なので、図1の表を作成する。
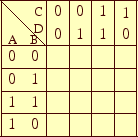
図 1: カルノー図を作成するための表(4変数)。
この表の縦および横は、それぞれの論理変数の値を示す。
ただし、真理値表と論理変数の並びが異なる。
真理値表は、2進数で値の小さい順に並んでいた。
しかし、カルノー図は、グレイコードで並んでいる。
この表は特殊で、上の端のセルと下の端のセル、右端のセルと左端のセルは連続していると考える。
グレイコードの場合、そのビットで表せる最大の数と最小の数は1ビットしか異なっていない。
表の枠が出来たならば、その中に論理変数に応じた論理式の値を入れていく。
今回の式の右辺は、5個の項から出来ている。
その5個の項のうち、どれかが1になった場合、論理式の値が1になる。
論理式が1になる論理変数(A, B, C, D)の値を探す。今後、論理変数の値はこの並びとする。
右辺第1項の値が1になるのは、(0, 1, 0, 0)の場合のみである。
そこで、それに対応するセル2行1列に1を書き込む。
右辺第2項の場合、A の項が無いのでそれは0でも1でも良く、(0, 1, 0, 1) と(1, 1, 0, 1)のとき
論理式の値が1になる。これも、表に1を書き込む。
同様に右辺第3項は、(1,0,1,1)第4項は(1,0,1,1)と(1,1,1,1) 、
第5項は(0,1,1,1)と(1,1,1,1)のとき論理式の値が1となります。
それぞれ1を書き込む。
次に、この表の中の全ての1を出来るだけ数の少ない正方形を含む長方形(ループ)で囲みます。
ただし、囲む場合、次の条件に従う。
- 囲んだ長方形の中のセルは、全て1であること。
- 囲んだ長方形の中のセルの数は、1,2,4,8,... のように 2Nであること。
- 同じセルを2つ以上のループで共有しても良い。
- カルノー図の上下の端、および左右の端は連続していると考える。
囲んだ結果を、図2に示す。3個のループで、囲まれたことになる。
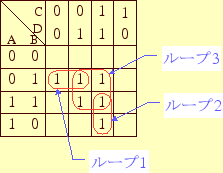
図 2: カルノー図の例
最後に、この3個のループから共通変数を取り出しその論理積を作る。
それぞれの論理積の論理和をとり、論理式を作る。
これが簡略化された論理式となる。
図2のループ1の共通変数の論理積は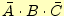 である。
ループ2の場合は
である。
ループ2の場合は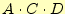 、
ループ3の場合は
、
ループ3の場合は となる。
これらの論理和は、
となる。
これらの論理和は、
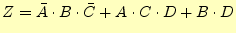
となる。これが、元の論理式を簡略化した結果である。
論理式の簡単化:カルノー図法
- カルノー図は、論理式や真理値表と同様に論理の表現法の一つ。
- 共通項で括るときに(A + A)の形になる括り方を見つけやすい。
- 入力変数の数により枠の取り方が異なる。3変数と4変数の場合を下図に示す。
図 カルノー図の枠の取り方
- 枠外の0や1は、行や列に割り当てられた変数の値を示す。
- 隣り合った枠の変数の値が一つだけ異なるようにするため、2進数とは違った順序となることに注意。
(このような順序のコードを
グレイコードという)
- 下図は、各枠がどの変数の値の組合せになるかを3変数の例で示したものである。
- 書き込む出力の値は、普通1のみで、出力が0のときは空白とする。
- 真理値表から書き込むときは、入力変数の値が同じとなる枠に、出力の値を書き込む。
- 論理式は加法標準形から書き込み、ANDの形の各項に相当する枠に1を書き込む。
項の中の の付く変数の値は0、
の付かない変数の値は0と考える。
- 下図に、各枠がどの論理式に対応するかを3変数の例で示す。
カルノー図の使用例
- 下の左に示す真理値表をカルノー図にした結果をその右に示す。
真理値表 カルノー図
真理値表の行をクリックすると、
その行およびカルノー図の対応したセルの背景色が黄色に変わり、
真理値表の行とカルノー図の対応が分かります。
【簡単化した論理式の導出】
- いくつかの1をまとめて1つの項を作り出す。
- 上下、左右の隣り合った領域をサークルとできる。
隣り合った枠は、どれか1つの変数の値が異なっているので、論理式に直した場合、
(A+A)のような形ができて、値が異なっている変数を省略できる。
- 1の枠は全てサークルにとらねばならない。
- サークルを構成する1の数は、2n個で、かつ最大数とする。
すなわち、1, 2, 4, 8, 16 のいずれかでなければならない。
- ひとつの1を何回サークルにとってもよい。
- 右端と左端の列は隣り合っているとする。
同様に、最上段の行と最下段の行は隣り合っているとする。
真理値表 カルノー図
|
① A・B・C+A・B・C
= A・C (B+B)
= A・C
② B・C
Q = A・C + B・C
|
練習問題
- 右端にあるボタンを "枠", "ラベル", "数値", "サークル", "結果" の
順に一つずつ押してください。カルノー図を使って、論理式の簡単化を
行う手順が確認できます。
- 論理式のどれかひとつの項をクリックしてみてください。
その項の文字の色が赤に代わり、
カルノー図の対応するセルの背景色が黄色になります。
これで、論理式の各項とセルの対応関係が分かります。
後の問題では、一つの項が2つとか4つのセルに対応することがありますが、
これも確認できます。
この問題はカルノー図を使わなくても簡単に解ける。
この問題はカルノー図を使わなくても簡単に解ける。
この問題はカルノー図を使わなくても簡単に解ける。
練習問題
次の真理値表をカルノー図を使って簡単化した論理式に直せ。
a.
出力Q=0の行の方が少ないので、Qに対する式
Q = B・C
から、ド・モルガンの定理を使って
Q = B+C
を得ることもできる。
b.
c.
d.
e.
f.
g.
小テスト解説
問7.
問10.
今回の問題はカルノー図を使う問題ではないが、
参考までに、カルノー図を使った方法も述べる。
問7-8.
問9-10.
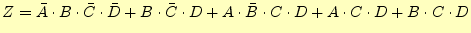 (1)
(1)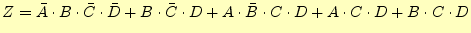 (1)
(1)

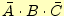 である。
ループ2の場合は
である。
ループ2の場合は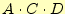 、
ループ3の場合は
、
ループ3の場合は となる。
これらの論理和は、
となる。
これらの論理和は、