| 丂嘆 01010000 | 丂嘇 01010001 | 丂嘊 01010010 | 丂嘋 01010011 |
[摎丗3] 2 偺曗悢傪媮傔傟偽偄偄丅
10101110偺0偲1傪斀揮偡傞偲丄01010001丅偙傟偵1傪壛偊丄01010010丅
| 丂嘆 0.12 | 丂嘇 0.55 | 丂嘊 0.75 | 丂嘋 0.84 |
[摎丗3] 12/16
| 丂嘆 俙 | 丂嘇 俛 | 丂嘊 俙 | 丂嘋 俛 | 丂嘍 俙亄俛 |
[摎丗5] 俙亄俙丒俛亖
俙丒乮侾亄俛乯亄俙丒俛亖
俙亄俙丒俛亄俙丒俛亖俙亄俛
| 丂嘆 A | 丂嘇 C | 丂嘊 A丒C | 丂嘋 A亄C | 丂嘍 A亄1亄C |
[摎丗4] A亄C 傪傑偲傔偰堦曄悢倃偲峫偊偰丄媧廂懃傪巊偆丅
| 丂嘆 A | 丂嘇 B | 丂嘊 A亄B | 丂嘋 1 | 丂嘍 0 |
[摎丗1] A亄A丒B亖A丒(1亄B)亖A丒1亖A
| 丂嘆 A亄B | 丂嘇 A亄B | 丂嘊 A丒B亄A丒B | 丂嘋 A丒B亄A丒B | 丂嘍 A亄B |
[摎丗4]
| 丂嘆 A | 丂嘇 2丒A | 丂嘊 A | 丂嘋 1 | 丂嘍 0 |
[摎丗4]
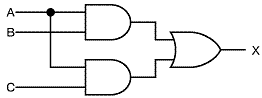
| 丂嘆 X亖A丒B亄C | 丂嘇 X亖A丒乮B亄C乯 | 丂嘊 X亖A亄B亄C | 丂嘋 X亖A丒B丒C |
[摎丗2]
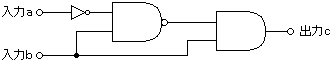
| 丂嘆 c亖a | 丂嘇 c亖a丒b | 丂嘊 c亖a亄b | 丂嘋 c亖a亄b | 丂嘍 c亖b |
[摎丗2]c=伿(a丒b)丒b=(a亄b)丒b=a丒b
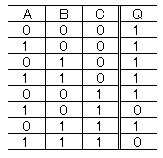
| 丂嘆 Q亖A亄B亄C | 丂嘇 Q亖A亄B丒C | 丂嘊 Q亖A亄B丒C | 丂嘋 Q亖A亄C | 丂嘍 Q亖A亄B丒C |
[摎丗4]
Q亖A丒B丒C亄A丒B丒C亖A丒C丂佀 Q亖A丒C亖A亄C