問1．10 進数の 25 を 8 ビットの 2 進数で表したものはどれか。
　① 00100101 　② 10000101 　③ 00011001 　④ 00100110 　⑤ 00101010

[答: 3] 25＝16＋8＋1＝2⁴＋2³＋2⁰
問2．２進数の 1011 と 1101 を加算した結果を 10 進数で表したものはどれか。
　① 16 　② 18 　③ 22 　④ 24 　⑤ 26

[答：4]
問3．２進数の 1.1011 と 1.1101 を加算した結果を 10 進数で表したものはどれか。
　① 3.1 　② 3.375 　③ 3.5 　④ 3.8 　⑤ 4.8

[答：3] (11.1000)₂ = (3.5)₁₀
問4．正の整数 n がある。 n を 5 進数として表現すると，1 の位の数字が 2 である 2 けたの数となる。また，n を 3 進数として表現すると，1 の位の数字は 0 となる。 n を10進数として表したものはどれか。
　① 10 　② 12 　③ 20 　④ 22 　⑤ 正解なし　⑥ 正解が二つ以上ある

[答：2] 10=20₅=101₃, 12=22₅=110₃ , 20=40₅, 22=42₅=211₃
問5． 16 進数 0.75 と等しいものはどれか。
① 2^－2＋2^－5＋2^－7＋2^－8
② 2^－2＋2^－3＋2^－4＋2^－6＋2^－8
③ 2^－1＋2^－2
④ 2^－1＋2^－2＋2^－3＋2^－4＋2^－6

[答：2] (0.75)₁₆ = (0.0111 0101)₂
問6．【正誤問題】10進数の 0.4 は2進数に変換しても有限小数となる。
　　① ○ 　　　　　　② ×
[答：2] 循環小数になる
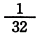問7．10 進数の分数を 16 進数の小数で表したものはどれか。
　① 0.01 　② 0.02 　③ 0.05 　④ 0.08 　⑤ 0.32

[答：4] 16進小数は a x 16^-1 + b x 16^-2 + … の形。この場合、1/32=8/256
問8．論理演算として、誤っているものはどれか。
　① １＋０＝１
　② ０＋１＝１
　③ １＋１＝２
　④ ０・１＝０
　⑤ 正解(間違っている式)なし
　⑥ 正解(間違っている式)が二つ以上ある

[答：3]
問9．10 進数の 25 を 8 進数で表したものはどれか。
　① 45 　② 65 　③ 31 　④ 46 　⑤ 52

[答: 3] 25＝24＋1＝3・8¹＋8⁰
問10．16 進数の 25 を 10 進数で表したものはどれか。
　① 16 　② 25 　③ 29 　④ 37 　⑤ 正解なし

[答: 4] 25₁₆＝2・16¹＋5・16⁰＝32＋5＝37