問1．4 ビットの２進数が二つあり、ビット毎の論理和が 1101 で、論理積が 0101 であるとき、これら二つの２進数の和を10進数で表すといくらか。

　① ８　　② ９　　③ １０　　④ １１　　⑤ １２　　⑥ １３　　⑦ １４　　⑧ １８　　⑨ ２０

[答：8]２、４番目は共に１、１番目は一方が１、３番目は共に０．５＋１３＝１８
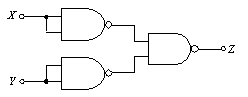
問2．NAND 回路による次の組合せ回路の出力 Z を表す式はどれか。

　① X・Y 　② X＋Y 　③ X＋Y 　④ X・Y 　⑤ X＋Y 　⑥ X・Y

[答：2]
問3．論理式 A ⊕ B と等価なものはどれか。
　① A＋B 　② A＋B 　③ A・B＋A・B 　④ A・B＋A・B 　⑤ A＋B

[答：3]A ⊕ B ＝￢(A・B＋A・B) ＝￢(A・B)・￢(A・B) ＝(A＋B）・(A＋B) ＝A・B＋A・B
問4．16 進数の小数 0.248 を10進数の分数で表したものはどれか。
　① 31/32 　② 31/125 　③ 41/125 　④ 73/512 　⑤ 124/125 　⑥ 31/256

[答：4]2/16 + 4/256 + 8/4096 = 1/8 + 1/64 + 1/512 = 73/512
問5. 論理式 A＋B＋B を簡単化したものはどれか。
　① A 　② A＋B 　③ B 　④ A 　⑤ A＋B 　⑥ A＋B

[答：5] A・B＋B ＝A・B＋(A＋1)・B ＝A・B＋A・B＋B ＝A・(B＋B)＋B ＝A＋B
問6．8 ビットの 2 の補数表現の 2 進数 11101101 を 10 進数に変換したものはどれか。

　① 109 　② 237 　③ 69 　④ -19 　⑤ -109 　⑥ 上記①～⑤のいずれでもない

[答:　4]
問7．論理式 A＋B＋A に等しいものはどれか。
　① A 　② B 　③ A 　④ 1 　⑤ 0 　⑥ A＋B 　⑦ 1＋B

[答:　4]
問8．図の論理回路と等価な論理式はどれか。

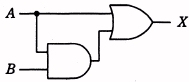
　① X＝A＋B 　② X＝A＋B 　③ X＝A＋B 　④ X＝A＋B 　⑤ X＝A

[答:　5]
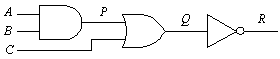
問9．図の論理回路において， A ＝1， B ＝0， C ＝1のとき， P ， Q ， R の値の適切な組合せはどれか。

　
　P　

　Q　

　R　

1　
0

1

0

2　
0

1

1

3　
1

0

1

4　
1

0

0

[答:　1]
問10．図の論理回路の論理式はどれか。

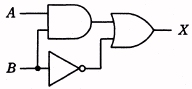
　① X＝A＋B 　② X＝A＋B 　③ X＝A＋B 　④ X＝A＋B 　⑤ X＝A

[答:　3]