| 問題および解答欄 | 採点欄 |
|---|---|
| 問1.10 進数の 55 を 16 進数で表わせ。[1点]
[答:3716, (37)16,
10進数とか2進数とかが明確なときは ()10、
()2 を省いてもいいが、紛らわしいときは、明示する。
この場合、 単に 37 は10進数か16進数か紛らわしい。] 55=3*16+7=(37)16
| |
| 問2.論理式 A+A・B+ Bを簡単化せよ。[1点]
[答: 1] カルノー図では4つのセルが全て1。
式では最初の2項がA+BになるからこのBと最後の項のBのORで1となる。
【別解】与式=A+ B+A・B X=A・Bと置くと 最初の2項はド・モアブルの定理からX。 従って全体は X+X=1となる 他にも求め方はある。 | |
問3.論理式 X=A・(B+C) と等価な回路図を書け。[2点]
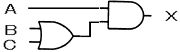 | |
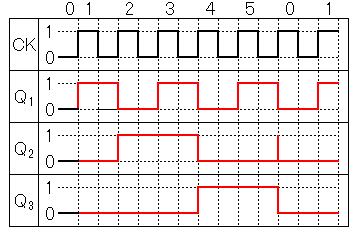
問4.下の回路図に回路を補い、クリア端子を利用した6進カウンタ回路として完成しなさい
ただし、初期値は0とし、クロック(clock)の立ち上がりで変化するものとする。
また、タイムチャートを完成しなさい。
[2点]
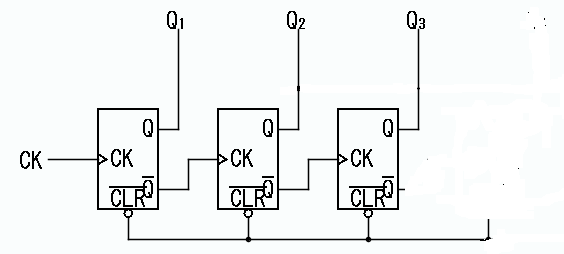 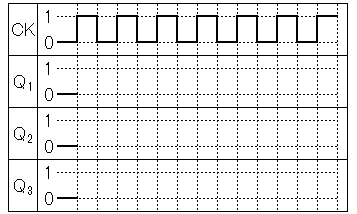
答:Q2とQ3をNANDゲートの入力として、
出力をCLR端子に繋ぐ
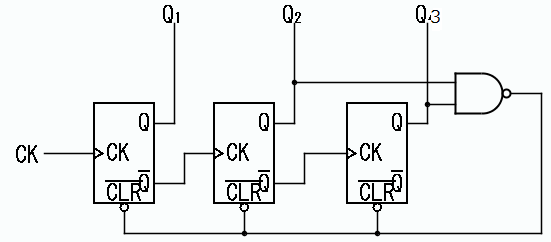  | |
問5.次の真理値表から論理式を導き、簡単化せよ。答えだけでなく、導出過程またはカルノー図を書くこと。[2点]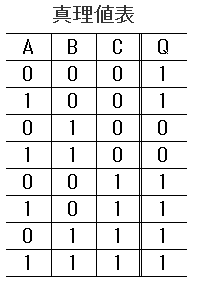
[答: Q = B+C]出力Q=0の行の方が少ないので、Qに対する式
Q = B・C から、ド・モルガンの定理を使って Q = B+C | |
問6.次の回路図を論理式で表し、簡単化せよ。答えだけでなく、導出過程を書くこと。[2点]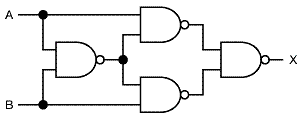 [答:A ⊕ B または A・B+A・B]
|