出力が前の状態に依存する回路を順序回路という。 順序回路を構成するには、新たな入力が加わらない限り現在の状態を維持し、 記憶し続ける回路が必要となる。これがフリップフロップ回路である[1]。
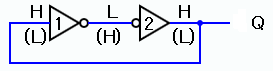
フリップフロップの原理回路は下図に示すようなNOT回路を2個直列 に接続してループ回路を構成したものである[1]。
もし、出力QがHレベルであったと仮定すると、 NOT1の入力には、Hレベルが加わる。 そのため、NOT1の出力はLレベルとなり、これがNOT2の入力となるから、 その出力QはHレベルとなり、最初の仮定と同じであり、安定状態となる。
一方、出力QをLレベルと仮定すると、全てのレベルが上とは逆になり、 やはり、Lレベルが安定状態となる。

図1.フリップフロップの原理図
上の説明では、電源をONにした最初の状態について言及していない。 また、遅延時間の存在についても触れていない。
NOT1とNOT2の最初の状態が共にHレベルであったと仮定する。 そうすると、NOT1,NOT2の入力は共にHレベルである。 二つのゲートの遅延時間が同じとすると、この遅延時間には NOT1,NOT2の出力は共にLレベルとなる。 すなわち、最初のHレベルからLレベルに変化している。 そして、さらに遅延時間後には共にHレベルに変化する。 このようにして発振状態となる。 下に、JavaScriptによるシミュレーションを示す。 二つのNOTゲートの出力の初期値は共にLレベルとし、 遅延時間は等しくしているため、無限に発振を続ける。 (二つのNOT回路の出力の初期値を相異なるレベルに選べば、発振は起こらない)
実際の回路では、電源を入れたときの状態は一般には決まっていない。 また、遅延時間は素子によってばらつきがある。 同じ素子でも、時間的に変動する。 このため、シミュレーションほど安定した発振が観測されるわけではない。
図1.はあくまで原理図であり、実際の回路を表したものではない。
因みに遅延時間を時たま乱数で変化させたシミュレーションを下に示す。 最初、発振が起きても、しばらくすると、発振が止まる。 再現性はなく、再読み込みする毎に異なる。
なお、下の回路(一般にループ一巡のインバータの個数が奇数のケース)では初期値に拘わらず、必ず発振が起きる。 ゲートの遅延時間も関係しないため、遅延時間を時間的に変動させて発振は止まらない。 もちろん、この回路はフリップフロップとは呼ばない。
ある時刻で入力がHレベル(1)であれば、遅延時間後の出力はLレベル(0)となる。 これが入力となるため、遅延時間後には出力はHレベル(1)になる。これを繰り返すので、発振状態が続く。
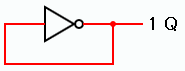
図2.ループ一巡のインバータの個数が奇数のケース
JavaScriptによるシミュレーションを下に示す。
一般には、回路に閉ループが含まれれば、発振を起こす可能性がある。 実用回路では、当然、無用な発振が起きないように、対策が取られる。
図3.にNORゲートによるRSフリップフロップ回路図とタイムチャートを示す。 R,S入力端子には周期の異なる(周期比3:2)矩形波信号を与えている。 全ての端子の初期値は0(Lレベル)としているので、初期状態では図1と等価である。 このため、発振する。
少し、時間が経過すると、R信号が1(Hレベル)となる。 そうすると、下のNORゲートの出力Qは上のNORゲートの出力 Qの値に関わりなく、0(Lレベル) となり、発振がとまり、 Q=1、Q=0となる。 その後、S,R信号の変化により真理値表にあるようにQ,Q の値が変化する。
数周期後にS信号とR信号が同時に1から0に変わる。 図1と等価な回路となる。 その直前ではQとQの値は共に0であるから、 発振が起きる。 (等価な回路となった直前でQとQの値が相異なるときは発振は起きない)
R-Sフリップフロップでは、S信号とR信号をともに1にすることは禁じられている。 これが守られれば、S信号とR信号が同時に1から0に変わるケースはあり得ない。 従って、正しい使い方をする限りにおいては、発振は起こらない。
S信号はONスイッチ、R信号はOFFスイッチである。 ONとOFFを同時に押すのはナンセンスということである。
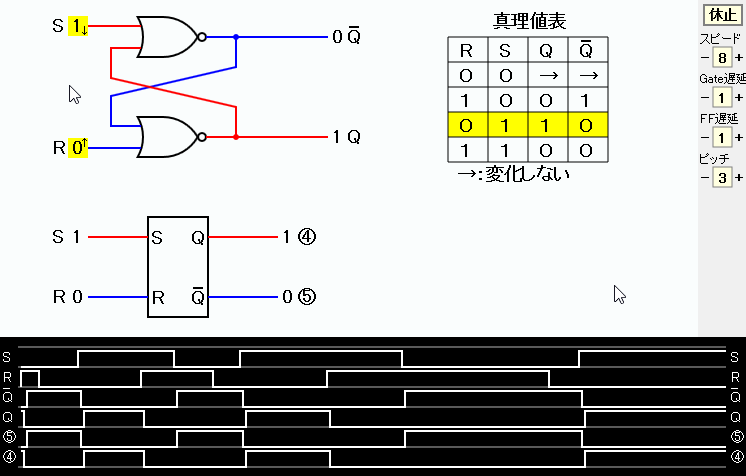
図3.RSフリップフロップ(ゲート遅延時間一定)
JavaScriptによるシミュレーションを下に示す。
この場合の発振は前の節で述べたように、 二つのNORゲートの遅延時間がぴったり一致していることにより継続する。 遅延時間がずれると止まる。図4にその様子を示す。 下のタイムチャート上では二度発振状態があるが、最初と次では、 状況が少し異なる。乱数で遅延時間を変化させているため、再現性はない。

図4.RSフリップフロップ(ゲート遅延時間変動)
JavaScriptによるシミュレーションを下に示す。
マスタースレーブJKフリップフロップの回路図とタイムチャートを図5に示す。 各ゲートの遅延時間は乱数を用いて少し時間的に変動させている。 また、全てのゲートの初期値を0としている。 最初に、発振しているが、数サイクルで安定状態になっている。 この後は再び発振することはない。 クロック信号CKが1から0に変化する(クロックの立下り)ときの直前のJ,K,Q,Qの値により、 、次のQ,Qの値が決まる。

図5.マスタースレーブJKフリップフロップ
JavaScriptによるシミュレーションを下に示す。
このマスタースレーブJKフリップフロップ回路は閉ループを構成するゲートの初期値が同じで、 ゲートの遅延時間が同じであれば、止まることなく、発振が続く。
一方、 別のページでのマスタースレーブJKフリップフロップ回路 では、ゲートの初期値と遅延時間は同じであるが、発振は起きない。
入力側のマスターフリップフロップへのS入力は最初の2入力ANDゲートで J・Q が計算され、R-S-Tフリップフロップの内部でこの結果とクロック信号CKとANDされる。
つまり、2入力ANDゲート2個で (J・Q)・CK が計算される。
一方、図5の回路では、3入力NANDゲートで J・Q・CK が計算される。
論理的には等価回路であるが、遅延時間を考慮すると、動作が異なる。
数学的に証明したわけではないが、いくつかのシミュレーション実験から、 この3信号のAND回路構成の違いで、一方では発振が起こり、他方では発振が起きないものと 推測される。
この回路には三つの閉ループがあり、12変数にもなるので、数学的証明は簡単ではないが、 気が向いた時にでも考えてみたい。
基本的なR-Sフリップフロップはわずか2個のゲートで構成できるが、 マスタースレーブJKフリップフロップ回路は9個のゲートとなり、 R-Sフリップフロップより格段に複雑である。
これに対して、エッジトリガ型フリップフロップはフリップフロップ一段ですむ。 しかし、適切な幅のパルスを生成するのは簡単ではない。 エッジトリガJKフリップフロップとしてよく知られている回路は全体の回路規模は マスタースレーブJKフリップフロップ回路と同等である。
しかし、このエッジトリガJKフリップフロップでも発振が起きるかどうか、 そのタイムチャートに興味があるので、シミュレーションしてみよう。
エッジトリガJKフリップフロップの回路図とタイムチャートを図6に示す。 各ゲートの遅延時間は乱数を用いて少し時間的に変動させている。 また、全てのゲートの初期値を0としている。 最初に、発振することがあるが、数サイクルで安定状態になっている。 この後は再び発振することはない。
遅延時間を同じとしたときは、発振し、J, Kの値を変えても発振は止まらない。
入力、出力信号のほか、ゲート⑤、ゲート⑥のタイムチャートを観測している。 この回路はクロックの立ち上がりで動作する。
直接ゲートの出力にパルス状の信号が現れるわけではない。
JavaScriptによるシミュレーションを下に示す。