R-Sフリップフロップ

１．R-Sフリップフロップ(NOR回路使用)

Flip Flopというのはシーソーの動きを表す「ぎっこん ばったん」といった擬音語である。 RはReset、SはSetの頭文字である。

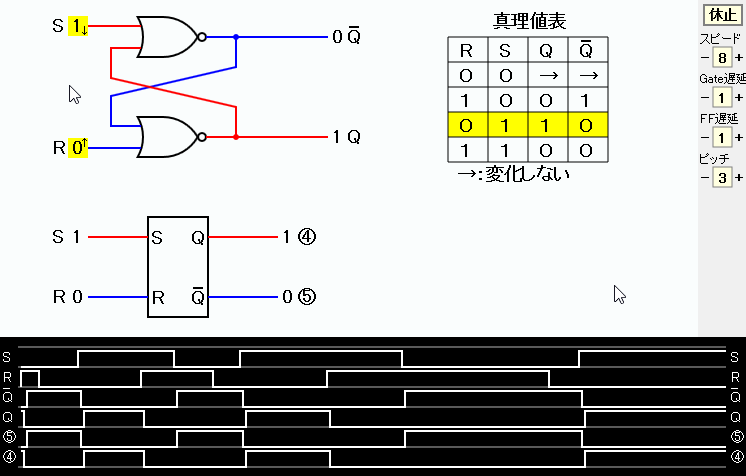
下にNOR回路使用を使用したR-Sフリップフロップを示す。 S-Rフリップフロップと呼ばれることもある。 信号の値を色で表す。青は０、赤は１を表す。 ORゲートの出力端子に否定マークが付いたものは、ORゲートの次にNOTゲートが続いた回路と等価であり、 NORゲートと呼ぶ（OR+NOT）。

フリップフロップは通常、回路図の下に示したような長方形に端子名を書いた形で表される。 動作は同じであるが、たまたま、ゲートの組み合わせ回路では上がQで下がQである。 一方、長方形記号では、通常、上から Q、Qの順に書くため、上と下が逆になっている。

回路図の下に、回路図の要所の信号の時間的な変化をグラフで表している。このような図をタイムチャートあるいはタイミングチャートと呼ぶ。

最初にこのページを開いたり、再読み込みすると、出力信号が激しく変化している（発振している）ことが分かる。 発振するわけは後で説明する。

入力信号線SかRをクリックすると、信号の値が反転し、発振は止まる。

【シミュレータの操作方法】

下のR-Sフリップフロップ回路のシミュレーションを例として、シミュレータの操作方法を述べます。 回路図の右の真理値表は回路図と連動して、行の背景色が黄色に変わります。 信号線の青は０、赤は１を表します。回路図の入力端子S,Rの横の １↓ あるいは０↑をマウスでクリックすると、 入力の値が反転し信号線の色が変わります。 図の右上の "休止"ボタンをマウスでクリックすると、シミュレーションが一時停止します。 表示は"Go !!"に変わります。もう一度押すとシミュレーションを再開します。 その他のボタンはここでは、特に操作する必要はありません。必要が生じたところで説明します。 回路図の下部にタイミングチャートを示しています。

フリップフロップの基本操作は、通常はS、Rとも 0（青）にしておく。 オンにするときは、クリックして、信号Sを１（赤）に変え、もう一度クリックして元の０（青）に戻す。 オフにする場合も同じで、信号Rを一旦赤に変え、すぐ、青に戻す。 押ボタンスイッチの要領である。ずっと押し続けるのではなく、押して離す。

R=0, S=0がスイッチで言えば OFF の状態を表す。 R が Resetスイッチ、S がSetスイッチに当る。
二つをともに ON にする(R=1, S=1)と、二つの出力端子の値が共に 1 となるが、 R-Sフリップフロップではこのような使い方は想定されていない。 （ONとOFFの押しボタンスイッチがあるとき、普通は、同時に両方押すような操作はしない。）

例えば、S=1 とすると Q=1, Q=0 となる （フリップフロップがONの状態）。 この後、S=0 に戻しても、出力端子の状態は変わらない。 このことが フリップフロップの唯一無二の特徴と言える。

フリップフロップがONの状態で、 S=1 (そのあと、S=0に戻す)としても状態は変わらないが、 R=1 (そのあと、R=0に戻す)とした場合には、 Q=0, Q=1 すなわちフリップフロップがOFFの状態に変わる。

次の回路では、入力S、Rに周期的に変化する信号を与えている。 この場合には、入力端子の数値をクリックして値を反転させることはできない。

この場合も、最初にこのページを開いたり、再読み込みすると、出力信号が発振する。 その後も入力信号S、Rが同時に１から０に変化したとき発振が起きる。

入力信号S、Rの周期は 50 : 40 の比に設定している。最小公倍数は200となるため、周期200で発振が起きる。 最小公倍数が大きくなる周期を選べば、発振の頻度は減少するが皆無とはならない。

２．R-Sフリップフロップ(NAND回路使用)

下にNAND回路使用を使用したR-Sフリップフロップを示す。 下図では、ORゲートの入力に否定マークがついたゲートを使用している。 これはゲート記号をANDに変え、否定マークを出力につけたものと等価である。 このため、このゲートもNANDゲート（AND+NOT）と呼ぶ。負論理で動作するため、否定マークを入力側に付ける。

この場合は、 S=1, R=1がスイッチで言えば OFF の状態を表す。 このページを最初に開いたときはS=0, R=0、 すなわち、二つのスイッチが共に ON の状態にある。実は、上で述べたように、 二つをともに ON にするような使い方は想定されていない。 （しかし、初期状態で、二つのスイッチが共に OFF の状態にあれば、NOR回路にR-Sフリップフロップと同様に、発振が起こる）
　例えば、S=0 とすると Q=1, Q=0 となる （フリップフロップがONの状態）。 この後、S=1 に戻しても、出力端子の状態は変わらない。
　フリップフロップがONの状態で、 S=0 (そのあと、1に戻す)としても状態は変わらないが、 R=0 (そのあと、1に戻す)とした場合には、 Q=0, Q=1 すなわちフリップフロップがOFFの状態に変わる。
注意：通常、下のNANDの出力をQで表わすが、 その信号の値は、上のNANDの出力の否定とは限らない。
上のNANDの出力 Q に注目すると
　　Q = S＋R・Q
となる。

　慣例に従い、上の図では、端子名そのものに Sのように、文字Sの上に棒線を引いているが、 入力信号の否定でなく、棒線を含めて、一つの文字記号である。 論理式の説明では、紛らわしいので、入力信号自体を S, R で表す。
現在の値と次の値を区別して書くと
　　Q_n+1 = S_n ＋ N_n
　　N_n+1 = R_n ＋ Q_n
となる。(下段のNANDの出力名を N とした)
R = 1, S = 1 のとき
　　Q_n+1 = 1
　　N_n+1 = 1
となり、発振は起こらない。
しかし、初期値が R = 1, S = 1 のときは
　　Q_n+1 = N_n
　　N_n+1 = Q_n
となる。
(Q₀,N₀)＝(0,0)の場合、
(Q₁,N₁)＝(1,1)、
(Q₂,N₂)＝(0,0)、
・・・
となり、発振する。