一つのページにJavaScriptで動く多くのシミュレーション回路を載せるとCPU負荷が高くなるので、ページを複数に分ける。
段数が多い非同期式カウンタは、クロック周波数が高くなると、遅延時間が無視できなくなり、 様々な問題が発生する可能性がある。 このため、一般には同期式カウンタが使用される。
同期式カウンタは非同期式に比べると回路が複雑になるが、 すべての FF が同時に動作するので非同期式に比べてすばやく動作する。
カウンタに限らずデジタル回路は大きく同期式と非同期式に分けられる。 回路の規模が小さいうちは非同期式が設計・製作ともに簡単にできるが、 回路規模が大きくなると遅延などの計算が複雑になるので、 規模の大きな回路は同期式で設計される。
Dフリップフロップはクロックが加わった瞬間にD入力の値を読み込んで出力する。 そこで、このとき各フリップフロップが出力しなければならない値を入力端子の値とする ことによって、カウンタを作ることができる。
例として5進カウンタを取り上げる。真理値表を下に示す。 カウンタの設計では、ある時刻の出力から次の時刻の入力を決めるため、 真理値表では出力データを左の欄にに、入力データを右の欄に書く方が分かりやすい。 5進カウンタでは出力の値は10進表記では 0, 1, 2, 3, 4, 0, 1, ... である。 5にはならず、4の次は0に戻る。
回路図では信号は左から右に流れるように書くため、左のほうが下位ビットに当たる。 このため、カウンタの出力は D1, D2, D3 の順では 000、100、010、110、001、000、100、... となる。このため表の1行目は 0の次は1 すなわち 000 100 となる(000の次は100)。 2行目は1の次は2すなわち 100 010 となる(100の次は010)。 このようにして3の次は4まで進む。
4の次は0であることに注意をする。
5進カウンタの場合、出力の値が5、6、7となることはないので、真理値表にはX印を書く。
| Q1 | Q2 | Q3 | D1 | D2 | D3 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | x | x | x |
| 0 | 1 | 1 | x | x | x |
| 1 | 1 | 1 | x | x | x |
この真理値表からD1,D2,D3をそれぞれ Q1,Q2,Q3を使ってなるべく簡単な式で表す。 一般的には、カルノー図を使うが、ここでは、論理式の簡単化(カット・アンド・トライ法)による。
カルノー図法による簡単化は別のページにまとめているのでここでは省略する。
D1に対する論理式を加法標準形で求めると、 グレーで示した二つの行から
D1 = Q1・Q2・Q3
+Q1・Q2・Q3
= Q1・Q3
(Q2+Q2)
= Q1・Q3
となる。
| Q1 | Q2 | Q3 | D1 | D2 | D3 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | x | x | x |
| 0 | 1 | 1 | x | x | x |
| 1 | 1 | 1 | x | x | x |
D2については下表に示す2行が選ばれ、
| Q1 | Q2 | Q3 | D1 | D2 | D3 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | x | x | x |
| 0 | 1 | 1 | x | x | x |
| 1 | 1 | 1 | x | x | x |
D2 = Q1・Q2・Q3
+Q1・Q2・Q3
= (Q1・Q2
+Q1・Q2)・Q3
= (Q1 ⊕ Q2)・Q3
となる。真理値表から Q1と Q2)の値が異なるときは、 Q3の値は常に 0 (Q3の値が常に 1 )であるから 上の式は更に簡単化され、
D2= Q1 ⊕ Q2
となる。 真理値表で「x」は 0 でも 1 でも良いことを表すので、 加法標準形では、これらの行は選んでも、選ばなくてもよい。 下に示すように、2行を追加して、論理式を簡単化すれば上と同じ結果が得られる。
| Q1 | Q2 | Q3 | D1 | D2 | D3 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | x | x | x |
| 0 | 1 | 1 | x | x | x |
| 1 | 1 | 1 | x | x | x |
D3については、下のように2行を選んで、式を簡単化すると
D3 = Q1・Q2
となる。
| Q1 | Q2 | Q3 | D1 | D2 | D3 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | x | x | x |
| 0 | 1 | 1 | x | x | x |
| 1 | 1 | 1 | x | x | x |
以上をまとめると、
D1 = Q1・Q3
D2 = Q1 ⊕ Q2
D3 = Q1・Q2
となる。そこで、クロックを共通にした3つのDフリップフロップに、上式で示される
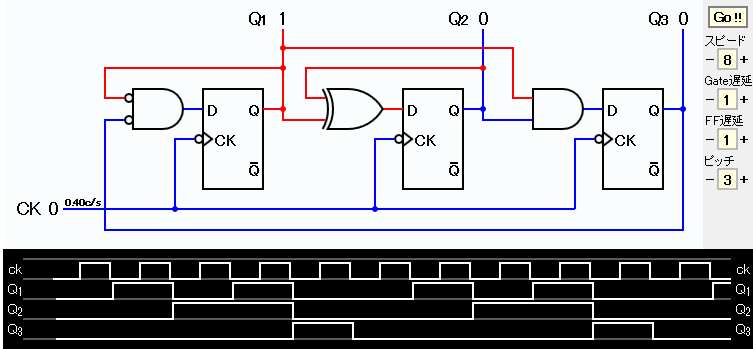
この回路のシミュレーションのスナップショットを下に示す。
タイムチャートでは右端が現在時刻となる。 回路図と同様に、Q1=1、Q2=0、Q2=0 となっていることが確認できる。
タイムチャートを左から見ると、 カウンタの値が10進で0、1、2、3、4、0、1、... と変化していることを確認できる。

JavaScriptで動作するシミュレーション回路を下に示す。
DフリップフロップはQ端子もあるから、こちらから出力をとれば、 左端のNORゲートはANDゲートに置き換えることができる。
Dフリップフロップによる3進同期カウンタを設計する。5進カウンタより、回路は簡単である。
| Q1 | Q2 | D1 | D2 | |
| 0 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 0 | |
| 1 | 1 | x | x |
×印の4行目は論理式の設計では使用してもいいし、使用しなくてもいい。
この真理値表の場合、D1に対しては 0、D2に対しては 1
とした方が論理式が簡単化される。
D1=Q1・Q2 ・・・1行目から
D2=Q1 ・・・2行目と4行目から
D2の場合、
2行目だけではQ1・Q2であるが、4行目も1と考えれば
Q1・Q2+Q1・Q2=
Q1となる。
Dフリップフロップによる4進同期カウンタを設計する。
| Q1 | Q2 | D1 | D2 | |
| 0 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 1 | |
| 0 | 1 | 1 | 1 | |
| 1 | 1 | 0 | 0 |
加法標準形から
D1=Q1・Q2+Q1・Q2=Q1 D2=Q1・Q2+Q1・Q2=Q1 ⊕ Q2となる。