同期式カウンタとはカウンタを構成する全てのフリップフロップが同じクロックで動作するものである。 Dフリップフロップを使う方法とJKフリップフロップを使う方がよく知られている。 Dフリップフロップでは、D入力だけを使うのに対して、JKフリップフロップ(JK-FF)ではJ入力とK入力を使用する。 二つ使うため設計は複雑になる(設計に使う真理値表が2倍になる)が、自由度が高くなることから、一般には、 フリップフロップの周辺に使うゲートを少なくすることができる。
JK-FFの現在のJ,K,Qの値と次の時刻におけるQの値(Q'で表す)の関係は以下の表の通りである。
| J | K | Q | Q' | |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 0 | |
| 1 | 1 | 0 | 1 | |
| 0 | 0 | 1 | 1 | |
| 1 | 0 | 1 | 1 | |
| 0 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 0 |
この表は次のように書き換えることもできる。x印はこの値には関係しないことを表す。
| 出力の変化 | J | K | |
|---|---|---|---|
| 0 → 0 | 0 | x | |
| 0 → 1 | 1 | x | |
| 1 → 0 | x | 1 | |
| 1 → 1 | x | 0 |
JK-FFによる同期式カウンタの設計では、J入力に対する回路とK入力に対する回路を独立して別々に作成する。 すなわち、設計方法の本質はD-FFの場合とまったく同じである。 D-FFによる同期式カウンタに比べると、設計に使用する真理値表はちょうど2倍になる。 上の表にあるように、0と考えて1と考えてもよい×印が多いため、自由度が高く、 このため、一般には、回路図が簡単になる。
JKフリップフロップによる3進同期式カウンタを設計する。最初に、次のような真理値表を作成する。
| Q1 | Q2 | Q1' | Q2' | J1 | K1 | J2 | K2 | ||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 1 | x | 0 | x | ||
| 1 | 0 | 0 | 1 | x | 1 | 1 | x | ||
| 0 | 1 | 0 | 0 | 0 | x | x | 1 | ||
| 1 | 1 | x | x | x | x | x | x |
左の列から説明する。最初のQ1、Q2は現在時刻でのJK-FFの出力の値を表す。 次のQ1'、Q2'は次の時刻におけるJK-FFの出力の値を表す。3進カウンタのため、 0の次が1、1の次が2、2の次が0である。3になることはないため、最後の行は x x とする。
次のJ1、K1は下位のJK-FFの入力を表す。 この欄に入る値がこの設計法の要となる。 まず、 J1、K1はQ1とQ1'に着目する。
次のJ2、K2は上位のJK-FFの入力を表す。上と同じように Q1とQ1'に着目して、J2、K2の列を埋めると、表が完成する。
回路設計は各列独立して行う。例えば、J1は真理値表を次のように捉える。
| Q1 | Q2 | J1 | |
|---|---|---|---|
| 0 | 0 | 1 | |
| 1 | 0 | x | |
| 0 | 1 | 0 | |
| 1 | 1 | x |
この場合、2行目の x を 1 と捉えて
J1=Q2
とする。
もちろん、カルノー図を使って求めてもよい。
同様に
J2=Q1となる。
K1、K2は、いずれも全ての行を1と考えることができるので、
K1=1、K2=1である。 2行ずつ選ぶと
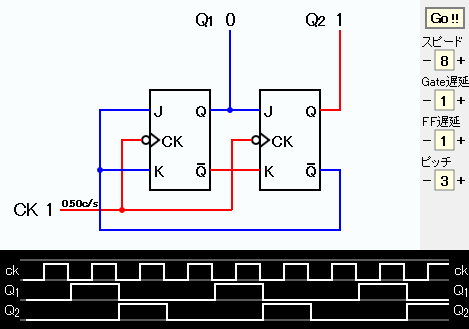
K1=Q2、 K2=Q1となる。 この場合も回路上余分なANDゲートやORゲートなどは要らない。 このときの回路図およびタイムチャート(画像)を下に示す。
タイムチャートからカウンタの出力が 0, 1, 2, 0, 1, ... となっていることを確認できる。

JavaScriptによるシミュレーションを下に示す。
JKフリップフロップによる4進同期式カウンタを設計する。最初に、次のような真理値表を作成する。
| Q1 | Q2 | Q1' | Q2' | J1 | K1 | J2 | K2 | ||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 1 | x | 0 | x | ||
| 1 | 0 | 0 | 1 | x | 1 | 1 | x | ||
| 0 | 1 | 1 | 1 | 1 | x | x | 0 | ||
| 1 | 1 | 0 | 0 | x | 1 | x | 1 |
J1、K1は、いずれも全ての行を1と考えることができるので、
J1=1、K1=1である。
J2、K2は、いずれも2行目と3行目を選ぶことができるので、
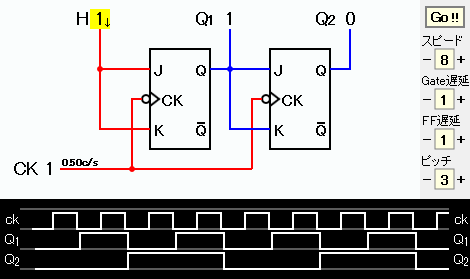
J2=Q1、K2=Q1となる。 このときの回路図およびタイムチャート(画像)を下に示す。
タイムチャートからカウンタの出力が 0, 1, 2, 3, 0, 1, ... となっていることを確認できる。
JavaScriptによるシミュレーションを下に示す。
JKフリップフロップによる5進同期式カウンタを設計する。最初に、次のような真理値表を作成する。
| Q1 | Q2 | Q3 | Q1' | Q2' | Q3' | J1 | K1 | J2 | K2 | J3 | K3 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | x | 0 | x | 0 | x | ||
| 1 | 0 | 0 | 0 | 1 | 0 | x | 1 | 1 | x | 0 | x | ||
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | x | x | 0 | 0 | x | ||
| 1 | 1 | 0 | 0 | 0 | 1 | x | 1 | x | 1 | 1 | x | ||
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | x | 0 | x | x | 1 | ||
| 1 | 0 | 1 | x | x | x | x | x | x | x | x | x | ||
| 0 | 1 | 1 | x | x | x | x | x | x | x | x | x | ||
| 1 | 1 | 1 | x | x | x | x | x | x | x | x | x |
カルノー図法による論理式の簡単化は別のページにまとめているのでここでは省略する。 結果を以下に示す。
J1=Q3 K1=1またはQ1または Q3 J2=Q1 K2=Q1 J3=Q1・Q2 K3=1またはQ1または Q2
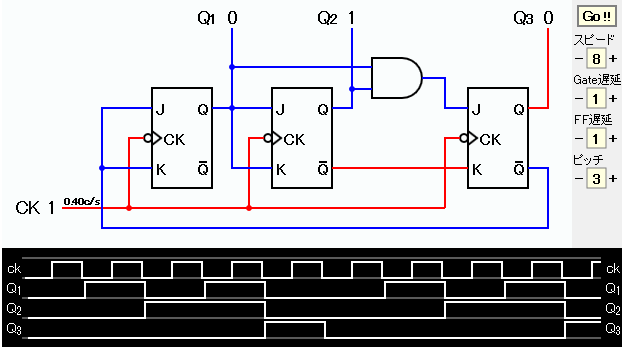
K1、K3の表し方は3通りある。 ここでは、回路図が見やすいものを選んだ。 回路図およびタイムチャートの画像コピーを下に示す。
タイムチャートからカウンタの出力が 0, 1, 2, 3, 4, 0, 1, ... となっていることを確認できる。
JavaScriptによるシミュレーションを下に示す。
JKフリップフロップによる6進同期式カウンタを設計する。最初に、次のような真理値表を作成する。
| Q1 | Q2 | Q3 | Q1' | Q2' | Q3' | J1 | K1 | J2 | K2 | J3 | K3 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | x | 0 | x | 0 | x | ||
| 1 | 0 | 0 | 0 | 1 | 0 | x | 1 | 1 | x | 0 | x | ||
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | x | x | 0 | 0 | x | ||
| 1 | 1 | 0 | 0 | 0 | 1 | x | 1 | x | 1 | 1 | x | ||
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | x | 0 | x | x | 0 | ||
| 1 | 0 | 1 | 0 | 0 | 0 | x | 1 | 0 | x | x | 1 | ||
| 0 | 1 | 1 | x | x | x | x | x | x | x | x | x | ||
| 1 | 1 | 1 | x | x | x | x | x | x | x | x | x |
カルノー図法による論理式の簡単化は別のページにまとめているのでここでは省略する。 結果を以下に示す。
J1=Q1または1 K1=Q1または1 J2=Q1・Q3 K2=Q1 J3=Q1・Q2 K3=Q1
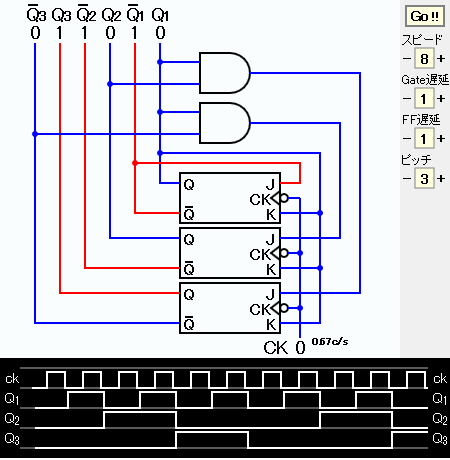
J1、K1の表し方は2通りある。 ここでは、回路図が見やすいものを選んだ。 回路図およびタイムチャートの画像コピーを下に示す。
タイムチャートからカウンタの出力が 0, 1, 2, 3, 4, 5, 0, 1, ... となっていることを確認できる。
JavaScriptによるシミュレーションを下に示す。
JKフリップフロップによる7進同期式カウンタを設計する。最初に、次のような真理値表を作成する。
| Q1 | Q2 | Q3 | Q1' | Q2' | Q3' | J1 | K1 | J2 | K2 | J3 | K3 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | x | 0 | x | 0 | x | ||
| 1 | 0 | 0 | 0 | 1 | 0 | x | 1 | 1 | x | 0 | x | ||
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | x | x | 0 | 0 | x | ||
| 1 | 1 | 0 | 0 | 0 | 1 | x | 1 | x | 1 | 1 | x | ||
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | x | 0 | x | x | 0 | ||
| 1 | 0 | 1 | 0 | 1 | 1 | x | 1 | 1 | x | x | 0 | ||
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | x | x | 1 | x | 1 | ||
| 1 | 1 | 1 | x | x | x | x | x | x | x | x | x |
カルノー図法による論理式の簡単化は別のページにまとめているのでここでは省略する。 結果を以下に示す。
J1=Q2+Q3 K1=Q1または1 J2=Q1 K2=Q1+Q3 J3=Q1・Q2 K3=Q2
K1の表し方は2通りある。 ここでは、回路図が見やすいものを選んだ。 回路図およびタイムチャートの画像コピーを下に示す。
タイムチャートからカウンタの出力が 0, 1, 2, 3, 4, 5, 6, 0, 1, ... となっていることを確認できる。
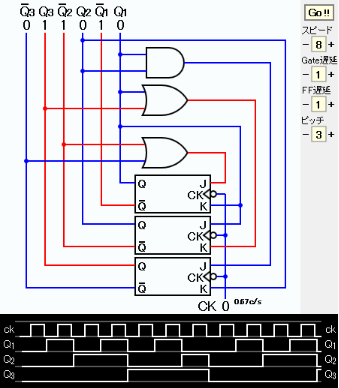
JavaScriptによるシミュレーションを下に示す。
JKフリップフロップによる8進同期式カウンタを設計する。最初に、次のような真理値表を作成する。
| Q1 | Q2 | Q3 | Q1' | Q2' | Q3' | J1 | K1 | J2 | K2 | J3 | K3 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | x | 0 | x | 0 | x | ||
| 1 | 0 | 0 | 0 | 1 | 0 | x | 1 | 1 | x | 0 | x | ||
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | x | x | 0 | 0 | x | ||
| 1 | 1 | 0 | 0 | 0 | 1 | x | 1 | x | 1 | 1 | x | ||
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | x | 0 | x | x | 0 | ||
| 1 | 0 | 1 | 0 | 1 | 1 | x | 1 | 1 | x | x | 0 | ||
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | x | x | 0 | x | 0 | ||
| 1 | 1 | 1 | 0 | 0 | 0 | x | 1 | x | 1 | x | 1 |
カルノー図法による論理式の簡単化は別のページにまとめているのでここでは省略する。 結果を以下に示す。
J1=Q1または1
K1=Q1または1
J2=Q1
K2=Q1
J3=Q1・Q2
K3=Q1・Q2
J1、K1の表し方は2通りある。 ここでは、回路図が見やすいものを選んだ。 回路図およびタイムチャートの画像コピーを下に示す。
タイムチャートからカウンタの出力が 0, 1, 2, 3, 4, 5, 6, 7, 0, 1, ... となっていることを確認できる。
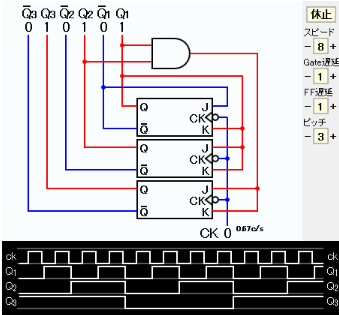
JavaScriptによるシミュレーションを下に示す。
JKフリップフロップによる9進同期式カウンタを設計する。最初に、次のような真理値表を作成する。
| Q1 | Q2 | Q3 | Q4 | Q1' | Q2' | Q3' | Q4' | J1 | K1 | J2 | K2 | J3 | K3 | J4 | K4 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | x | 0 | x | 0 | x | 0 | x | ||
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | x | 1 | 1 | x | 0 | x | 0 | x | ||
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | x | x | 0 | 0 | x | 0 | x | ||
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | x | 1 | x | 1 | 1 | x | 0 | x | ||
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | x | 0 | x | x | 0 | 0 | x | ||
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | x | 1 | 1 | x | x | 0 | 0 | x | ||
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | x | x | 0 | x | 0 | 0 | x | ||
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | x | 1 | x | 1 | x | 1 | 1 | x | ||
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | x | 0 | x | 0 | x | x | 1 | ||
| 1 | 0 | 0 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | ||
| 0 | 1 | 0 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | ||
| 1 | 1 | 0 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | ||
| 0 | 0 | 1 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | ||
| 1 | 0 | 1 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | ||
| 0 | 1 | 1 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | ||
| 1 | 1 | 1 | 1 | x | x | x | x | x | x | x | x | x | x | x | x |
カルノー図法による論理式の簡単化は別のページにまとめているのでここでは省略する。 結果を以下に示す。
J1=Q4 K1=Q1または1 J2=Q1 K2=Q1 J3=Q1・Q2 K3=Q1・Q2 J4=Q1・Q2・Q3 K4=Q1,Q2,Q3,Q4, or 1
K1、K4の表し方は2通り以上ある。 ここでは、回路図が見やすいものを選んだ。 回路図およびタイムチャートの画像コピーを下に示す。
タイムチャートからカウンタの出力が 0, 1, 2, 3, 4, 5, 6, 7, 8, 0, 1, ... となっていることを確認できる。
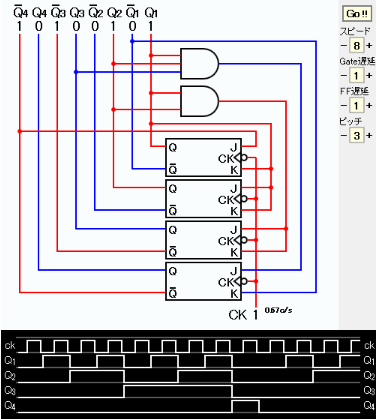
JavaScriptによるシミュレーションを下に示す。
JKフリップフロップによる10進同期式カウンタを設計する。最初に、次のような真理値表を作成する。
| Q1 | Q2 | Q3 | Q4 | Q1' | Q2' | Q3' | Q4' | J1 | K1 | J2 | K2 | J3 | K3 | J4 | K4 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | x | 0 | x | 0 | x | 0 | x | ||
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | x | 1 | 1 | x | 0 | x | 0 | x | ||
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | x | x | 0 | 0 | x | 0 | x | ||
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | x | 1 | x | 1 | 1 | x | 0 | x | ||
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | x | 0 | x | x | 0 | 0 | x | ||
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | x | 1 | 1 | x | x | 0 | 0 | x | ||
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | x | x | 0 | x | 0 | 0 | x | ||
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | x | 1 | x | 1 | x | 1 | 1 | x | ||
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | x | 0 | x | 0 | x | x | 0 | ||
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | x | 1 | 0 | x | 0 | x | x | 1 | ||
| 0 | 1 | 0 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | ||
| 1 | 1 | 0 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | ||
| 0 | 0 | 1 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | ||
| 1 | 0 | 1 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | ||
| 0 | 1 | 1 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | ||
| 1 | 1 | 1 | 1 | x | x | x | x | x | x | x | x | x | x | x | x |
カルノー図法による論理式の簡単化は別のページにまとめているのでここでは省略する。 結果を以下に示す。
J1=Q1 or 1 K1=Q1 or 1 J2=Q1・Q4 K2=Q1 J3=Q1・Q2 K3=Q1・Q2 J4=Q1・Q2・Q3 K4=Q1
J1、K1の表し方は2通りある。 ここでは、回路図が見やすいものを選んだ。 回路図およびタイムチャートの画像コピーを下に示す。
タイムチャートからカウンタの出力が 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, ... となっていることを確認できる。
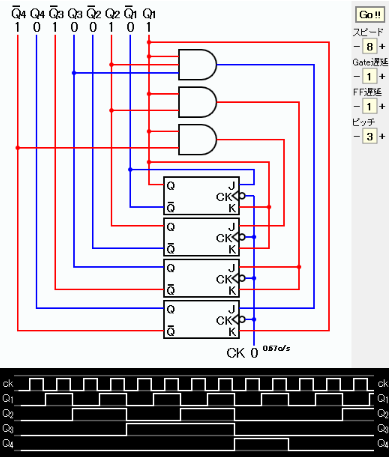
JavaScriptによるシミュレーションを下に示す。
JKフリップフロップによる11進同期式カウンタを設計する。最初に、次のような真理値表を作成する。
| Q1 | Q2 | Q3 | Q4 | Q1' | Q2' | Q3' | Q4' | J1 | K1 | J2 | K2 | J3 | K3 | J4 | K4 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | x | 0 | x | 0 | x | 0 | x | ||
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | x | 1 | 1 | x | 0 | x | 0 | x | ||
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | x | x | 0 | 0 | x | 0 | x | ||
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | x | 1 | x | 1 | 1 | x | 0 | x | ||
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | x | 0 | x | x | 0 | 0 | x | ||
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | x | 1 | 1 | x | x | 0 | 0 | x | ||
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | x | x | 0 | x | 0 | 0 | x | ||
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | x | 1 | x | 1 | x | 1 | 1 | x | ||
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | x | 0 | x | 0 | x | x | 0 | ||
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | x | 1 | 1 | x | 0 | x | x | 0 | ||
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | x | x | 1 | 0 | x | x | 1 | ||
| 1 | 1 | 0 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | ||
| 0 | 0 | 1 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | ||
| 1 | 0 | 1 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | ||
| 0 | 1 | 1 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | ||
| 1 | 1 | 1 | 1 | x | x | x | x | x | x | x | x | x | x | x | x |
カルノー図法による論理式の簡単化は別のページにまとめているのでここでは省略する。 結果を以下に示す。
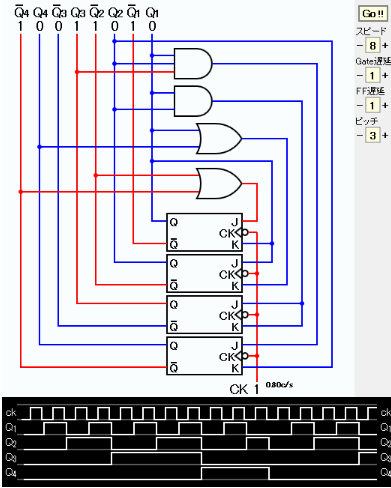
J1=Q2+Q4 K1=Q1 or 1 J2=Q1 K2=Q1+Q4 J3=Q1・Q2 K3=Q1・Q2 J4=Q1・Q2・Q3 K4=Q2
回路図およびタイムチャートの画像コピーを下に示す。
タイムチャートからカウンタの出力が 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0, 1, ... となっていることを確認できる。
JavaScriptによるシミュレーションを下に示す。
JKフリップフロップによる12進同期式カウンタを設計する。最初に、次のような真理値表を作成する。
| Q1 | Q2 | Q3 | Q4 | Q1' | Q2' | Q3' | Q4' | J1 | K1 | J2 | K2 | J3 | K3 | J4 | K4 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | x | 0 | x | 0 | x | 0 | x | ||
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | x | 1 | 1 | x | 0 | x | 0 | x | ||
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | x | x | 0 | 0 | x | 0 | x | ||
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | x | 1 | x | 1 | 1 | x | 0 | x | ||
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | x | 0 | x | x | 0 | 0 | x | ||
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | x | 1 | 1 | x | x | 0 | 0 | x | ||
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | x | x | 0 | x | 0 | 0 | x | ||
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | x | 1 | x | 1 | x | 1 | 1 | x | ||
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | x | 0 | x | 0 | x | x | 0 | ||
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | x | 1 | 1 | x | 0 | x | x | 0 | ||
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | x | x | 0 | 0 | x | x | 0 | ||
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | x | 1 | x | 1 | 0 | x | x | 1 | ||
| 0 | 0 | 1 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | ||
| 1 | 0 | 1 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | ||
| 0 | 1 | 1 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | ||
| 1 | 1 | 1 | 1 | x | x | x | x | x | x | x | x | x | x | x | x |
カルノー図法による論理式の簡単化は別のページにまとめているのでここでは省略する。 結果を以下に示す。
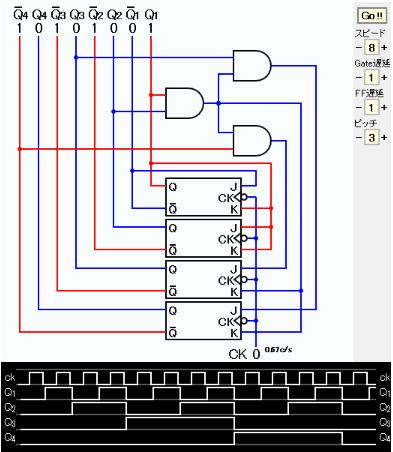
J1=Q1 or 1 K1=Q1 or 1 J2=Q1 K2=Q1 J3=Q1・Q2・Q4 K3=Q1・Q2 J4=Q1・Q2・Q3 K4=Q1・Q2
回路図およびタイムチャートの画像コピーを下に示す。
タイムチャートからカウンタの出力が 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 0, 1, ... となっていることを確認できる。
JavaScriptによるシミュレーションを下に示す。