OSM(OpenStrreMap)の海岸線データを繋ぎ合わせて、陸地ポリゴンを形成できた。 しかし、特に大陸は巨大なポリゴンとなるため、 これを zoom 7, 8程度のタイルの大きさを目安として、多数の小さなポリゴンに分割したい。
海岸線を含まない完全な陸地は、ポリゴンレコードとはせず、一括管理する。
海岸線を含むタイルをポリゴンとする。大抵は一つのポリゴンであるが、二つ以上のポリゴンが生まれるケースもある。
海岸線が通るタイルを見つけるだけであれば比較的簡単であるが、 ポリゴンを切り出すのが面倒である、
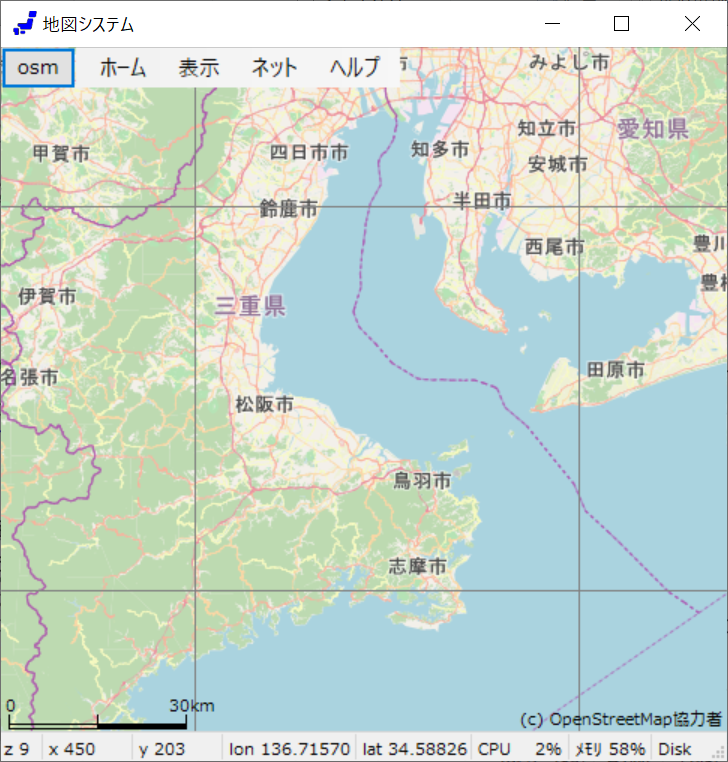
下図(zoom 9)では、ほぼ中央のタイルは本州の海岸線と6回交差している。従って、zoom 9 で分割する場合、 三つのポリゴンに分かれる。
ここでは本州の分割のみを考えるため、小さな島々は気にしなくてよい。
タイル分割を考えると、交差が4回以上になることは珍しくない。 分割は規則正しくタイル単位とする必要性はない。 しかし、何らかの規則性を保ち、交差を2回に限定するのは難しいであろう。
アルゴリズム的には記事[5]が参考になりそうである。
垂直線でポリゴンをスライスする。大きなポリゴンが一つと、小さなポリゴンが0個以上生まれる。 大きなポリゴンについては、可能であれば、後で、上部と下部をポリゴン、中間を矩形に3分割する。
OSM地図では OsmCoastline[2] による陸地ポリゴン分割データが広く使われているが、 ソースコードから推察すると、PostGISでポリゴンを分割している[3]ようである。
ポリゴンの簡単化も PostGIS であろう。
西から東へ縦方向にスライスする。zoom は取りあえず 7~10 とする。縦方向に長い場合、 上(北)と下(南)と中央の矩形に3分する。中央の矩形は可能な限り大きくする。
スライスでは大きなポリゴンが一つだけのときと小さなポリゴンが1つ以上切り出されることがある。
スライスにより、新しい頂点(分割線と海岸線との交点)が生まれる。
少なくともトーメンはマージン(オーバラップ)は考えない。
zoom 7でのスライスの場合、日本の本州は5つにスライスされる。 小さなポリゴンが生まれるが、その数は少ないであろう。
垂線と海岸線との交点の算出は線分同士の交点の算出よりは簡単である。
等間隔スライス近辺のノードを選ぶ。南北のノードの経度は一致しない。 それぞれ例えば中間点まで線分を引く。この線分が海岸線と交差する場合は、分割点にしない。
南北から伸びる線分の数は一般には異なるが、適当な水平線で繋ぐことにより、それぞれポリゴンを完成させる。
PostGIS の場合、南北に適当なノードを選んでこのような方法で分割しているのではなかろうか。
中間の矩形の高さが十分に大きい場合は、いずれ、複数の矩形に分割してもよい。
交差の有無の判定は java.awt.geom.Line2D のメソッド[6]を使用する。
最初のプログラムでは分割線は完全な垂線ではなく、南北の頂点を結ぶほぼ垂直な線分とする。
座標は int[] xs、int[] ys にある。最も西の経度は xs[ixmin]、東の経度は xs[ixmax] である。
北側の頂点は ixmin, ixmin+1, ... , ixmax である。
南側の頂点は ixmin, ixmin-1, ... , ixmax である。
末尾 xs.length-1 と先頭 0 は同じである。xs.length-1 の次は 1 である。0 の前は xs.length-2 である。
時計回り(北側)、反時計回り(南側で)、分割線を初めて超える頂点を求める。 南北の頂点を結ぶ線分を分割線とする。
この分割線が全線分と交わっていないことを確かめる。 交わりがあれば、南北二つの頂点からの線分は分割線とはならない。 分割線となった場合、分割されたポリゴンを出力する。
分割の成否にかかわらず、次の分割候補の頂点を求めて、同じことを繰り返す。
最初はなるべく簡単なプログラムでポリゴンが分割できるかどうかを調べる。
大陸によっては、垂直分割より、水平分割の方がよいケースもあるだろう。 また、日本の本州の場合、斜線の方がいい可能性がある。
ポリゴン分割は何年か前からの懸案であったが、その最初のプログラムである。
世界平面座標を (0, 0)~(230,230) としている。
まずは、分割候補となる南北ペアの頂点を求めた。
// ポリゴン分割の可能性を調べる
// -180 ~ 180度 ⇒ 0 ~ 2~30
int span = 1 << 21; // 3度弱
if ((xmax - xmin) >= 2*span) { // 大きなポリゴンだけを分割する
int ixNorth = ixmin;
int ixSouth = ixmin;
int bgn = (xmin / span) * span;
for (int x = bgn; x < xmax; x += span) {
// 北側のノード
while (xs[ixNorth] < x) {
if (ixNorth < xs.length-1) {
ixNorth++;
} else {
ixNorth = 1;
}
}
// 南側のノード
while (xs[ixSouth] < x) {
if (ixSouth > 0) {
ixSouth--;
} else {
ixSouth = xs.length - 2;
}
}
System.out.printf("x=%.2f(%d) 北%d 南%d ", (double)x/(1<<30), x, xs[ixNorth], xs[ixSouth]);
}
System.out.println();
}
南北頂点の座標は (xs[ixSouth], ys[ixSouth]) および (xs[ixNorth], ys[ixNorth]) である。
boolean linesIntersect(int[] xs, int[] ys, int xS, int yS, int xN, int yN) {
boolean fIntersect = false;
for (int i = 0; i < xs.length - 1; i++) {
if (java.awt.geom.Line2D.linesIntersect(xs[i], ys[i], xs[i+1], ys[i+1], xS, yS, xN, yN)) {
fIntersect = true;
break;
}
}
return fIntersect;
}
まず、次のようにして交差判定をした。-10、+10 は接しているものを交差とみなすかも知れないので、 頂点からずらした。Y座標は最北が 0 で、南に向かって数値が大きくなるため、南の頂点は北方向、 北の頂点は南方向に少しずらした。
結果は australia-oceania では交点なしとなるものが多いが、他は殆ど交点ありとなる。 海岸線が入り組んでいるため、そうなるのか、それともプログラムにバグがあるのか分からない。
交差がいつ起きたかを調べてみる。
boolean fIntersect = linesIntersect(xs, ys,
xs[ixSouth], ys[ixSouth]-10, xs[ixNorth], ys[ixNorth]+10);
このような簡単な方法では分割できないようである。