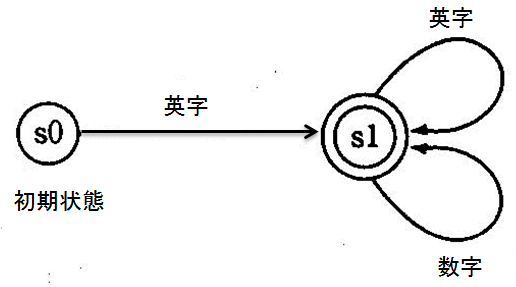
図1.識別子を認識する有限オートマトン
形式言語とオートマトンの関係を詳しく述べるために、チョムスキーの分類を再掲しておく。
| タイプ | 文法 | オートマトン | 言語例 |
|---|---|---|---|
| 0型 | 句構造文法 | チューリングマシン | 自然言語 |
| 1型 | 文脈依存文法 | 線形有界オートマトン | |
| 2型 | 文脈自由文法 | プッシュダウンオートマトン | プログラム言語 |
| 3型 | 正規文法 | 有限オートマトン | 体系化したコードなど |
識別子(変数名、関数名など)の構文規則は次のように正規文法により定義できる[1]。
<識別子> ::= <英字> { <英数字> } <英数字> ::= <英字> | <数字> <英字> ::= a | b | … | z | A | B | … | Z <数字> ::= 0 | 1 | 2 | … | 9
ここで { <英数字> } は <英数字> が0個以上並んだものを表す。 第2回の授業での記法を使えば、( <英数字> )* となる。
正規文法により定義された構文は有限オートマトン(finite automaton)によって認識することができる。 有限オートマトンは、有限個の状態と状態間の遷移を基本概念とする認識機械である。 初期状態から出発し、入力語中の記号を1つずつ読み込み、状態遷移を次々に繰り返し、 入力語が認識されるかどうかを調べる。上の構文規則で定義される識別子を認識する 有限オートマトンを図1.に示す。図中、○は状態を表し、矢印は状態遷移を表す。
初期状態s0で英字を読み込むと、状態s1に遷移する。 s1では、英字または数字の読み込みによって自分自身へ遷移する。 状態s1が◎になっているのは、それが識別子を認識した状態になっていることを表している。

この有限オートマトンの数学モデルは <Σ, S, s0, δ, F> の5要素から構成される。
プログラミング言語の構成要素は識別子のほか、 予約語(C言語で言えば、int, if, for, structなど)、演算子、記号、数値などが存在するが、 いずれも、正規文法で定義することができる。 したがって、コンパイラやインタプリタの字句解析フェーズでは、 このような有限オートマトンに対応する処理メカニズムを何らかの形で実現すればよい。