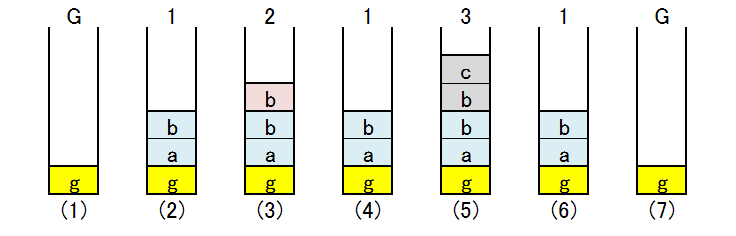
図.意味解析における記号表の動き
ここでは、中間コード(~アセンブリ言語コード)生成までを意味解析フェーズと呼び、 中間コードを機械語コードに変換するフェーズをコード生成フェーズと呼ぶことにする。
静的意味解析の内容としては、次のものがある。
次のC言語プログラムを例として、 識別子の適用範囲(スコープ)の解析について説明する。
┌─ プログラム ─────┐
int g = 2; | g |
int main() | |
{ // begin of block 1 |┌─ ブロック1 ───┐|
int a = 123, b = 10; || a, b ||
...... || ||
{ // begin of block 2 ||┌─ ブロック2 ─┐||
int b = 20; ||| b |||
...... ||| |||
} // end of block 2 ||└────────┘||
{ // begin of block 3 ||┌─ ブロック3 ─┐||
int b = 30, c = 40; ||| b, c |||
...... ||| |||
} // end of block 3 ||└────────┘||
} // end of block 1 |└──────────┘|
└────────────┘
ソースコードで "{" から "}" までをブロックと呼んでいる。 トップレベルで宣言された変数 g を大域的変数(global variable)、 ブロック内で宣言された変数 a, b を局所的変数(local variable)と呼ぶ。
グローバル変数は、固定データ領域に割り当てられ、全てのブロックから参照できる。 一方、ローカル変数は OS(operating system) が管理するスタック領域に割り当てられ、 定義されたブロック内だけで有効である。 従って、ブロック1で宣言されたローカル変数 a, b はブロック1、ブロック2、ブロック3で有効である。 しかし、変数名 b は重複しており、ブロック1だけでなく、ブロック2、ブロック3でも宣言されている。 このような場合、ブロック2、3では、それぞれ自分のブロックで宣言された変数 b が使われる。
意味解析では、ブロック表と記号表を使って変数の管理を行う。 概念的には、スタックと同じアルゴリズムが使われるので、下図を使って説明する。

例として、プログラム(の一部)
int a;
double b;
b = 3.1;
a = b * 2;
を考える。構文解析によって、概念的には次のような構文木と記号表が得られる。
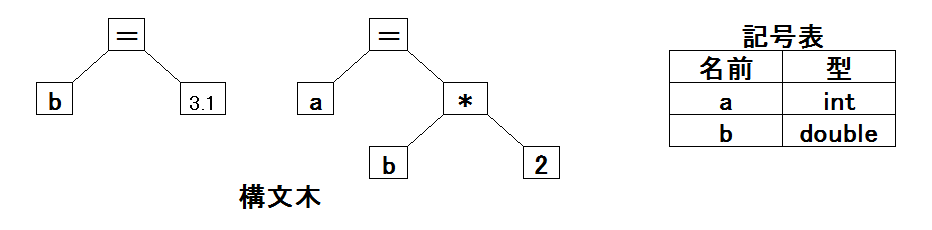
意味解析(semantics analysis)は、
構文木の意味を解釈するものである。
意味解析では各種のチェックも行われる。例えば、乗算演算子 "*" の右辺と左辺は共に 数値型(またはC言語の場合, char型のように、数値型に自動変換できるデータ型) でなければならない。代入演算子 "=" の場合、 左辺は右辺と同じデータ型(または自動変換できるデータ型)の変数でなければならない。 上の例では、b * 2 の計算結果(6.2)のデータ型は double型となる。 しかし、左辺の a のデータ型は int型のため、 自動的に整数型へのキャスト(すなわち a = (int)6.2)を中間コードが生成される。
しかし、 もし、char *a; ならば、
test01.c:6: cannot cast 'double' to 'char *'というコンパイラーエラーとなる。
ソースプログラム全体の構文解析が終わってから、
意味解析を行うというほうが、分かりやすいが、実際はそうでないことが多い。
構文解析ツールbisonの場合には、
bisonはアプリケーションプログラムをコンパイルするものではないが、 構文規則から、作り出されるものがC言語プログラムであるから、 中間言語がC言語であるという見方もできる。
再帰的下向き解析でも、構文規則毎に、構文解析と意味解析がセットとなっている。
意味解析によって作られるものを通常、 中間コード(木構造、逆ポーランド記法、三つ組、四つ組、Pコードなど)と呼ぶ。 制作演習では、意味解析ではアセンブリコードを生成するが、これが中間コードに当たる。
2 + 3 * 4 のように、"+" や "*" の演算子を被演算子の中に置く、 一般に使われている記法を中置記法(infix notation)という。 複雑な式では、(2 + 3) * 4 のように、括弧を用いて演算子の適用順序(計算順序)を指定する。
+ 2 * 3 4 のように、演算子を前に置く記法を前置記法(prefix notation) またはポーランド記法(Polish notation)という。 名称の由来は、ポーランド人の論理学者ヤン・ウカシェヴィチが考案したことによる。 '+'(2, '*'(3, 4)) と書いてみると、関数の書き方と似ていることがわかる。 括弧は使わず、(2 + 3) * 4 はポーランド記法では * + 2 3 4 と表わされる。
2 3 4 * + のように、演算子を後ろに置く記法を後置記法(postfix notation) または逆ポーランド記法(reverse Polish notation)という。 逆ポーランド記法の式は スタックを用いて簡単に計算できるので、 Hewlett-Packerd 社の関数電卓やコンパイラの中間コードなどに利用されている。 括弧は使わず、(2 + 3) * 4 は逆ポーランド記法では 2 3 + 4 * と表わされる。
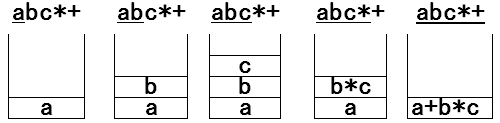
一般には後置記法が使われるため、後置記法を単にポーランド記法と呼ぶことも多い。後置記法による式 a b c * + の評価を考える[2]。 入力式を左から右に向かって調べる。まず、a の値をスタックに積む。 同様に、b、c の値をスタックに積む。つぎは演算子*である。 スタックに積んである b と c の値を取り出し、 この演算*を適用して、結果をスタックに積む。 次の入力は演算子+である。スタックに積んである二つの値を取り出し、 この演算+を適用して、結果をスタックに積む。 以上の操作はLR構文解析のshiftとreduceと同様である。
三つ組(triple)は、下のような形をしている。
(演算子, 被演算子, 被演算子)
被演算子は定数、変数、あるいは他の三つ組を指す。
式 a + b * c は次のように表現される。
① (*, b, c) ② (+, a, ①)②番目の三つ組中の①は、①番目の三つ組の結果を参照している。
四つ組(quadruple)という表現もある。これは、下のような形をしている。
(演算子, 被演算子, 被演算子, 結果)
式 a + b * c は次のように表現される。
(*, b, c, t1) (+, a, t1, t2)上の四つ組の結果(t1)を下の四つ組で被演算子として参照している。 下の四つ組の結果は t2 として参照される。
Pコード(Pseudo-Code: 擬似コード)は実際のマシン(コンピュータ)に依存した機械語命令の代わりに、 理想的な仮想マシン用の命令コードを指す。 JavaのバイトコードもPコードの一種とみなせるが、 Pコードと言えば、特に UCSD Pascal の P-Machine を指すことが多い。
Pコードマシンはスタック指向であり、ほとんどの命令がスタックからオペランドを持ってきて、 結果をスタックに戻す。例えば、add 命令はスタックの先頭2要素を取り出し、加算結果をスタックに戻す。 一部の命令は即値オペランドを持つ。
Pascalと同様、Pコードも型があり、ブーリアン(b)、文字(c)、整数(i)、実数(r)、集合(s)、ポインタ(a) が最初から用意されている。 以下に簡単な命令を示す。命令名、実行前のスタック状態、実行後のスタック状態、解説の順に並んでいる。
adi:(i1 i2)⇒ (i1+i2)、2つの整数の加算
adr:(r1 r2)⇒(r1+r2)、2つの実数の加算
dvi:(i1 i2)⇒(i1/i2)、整数の除算
inn:(i1 s1)⇒(b1)、メンバーシップを設定。
b1 には i1 が s1 のメンバーかどうかが設定される(true/false)。
idci i1:()⇒(i1)、整数定数をスタック上にロードする。
mov:(a1 a2)⇒()、メモリ間のコピー
not:(b1)⇒(~b1)、ブーリアンの否定
演算結果や関数の戻り値は常にレジスタ eax に置くものとする
再帰下向き構文解析法での2項演算のコード生成について述べる
例えば構文規則が Add ::= Mul "+" Mul の場合、
void add() {
mul(); // 被演算子1 のコード生成。結果は eax にセットされる。
code("push eax"); // 被演算子1の値をスタックにセーブしておく
mul(); // 被演算子2 のコード生成。結果は eax にセットされる。
code("pop ecx"); // セーブしていた被演算子1の値を取り出し、ecx にセットする
code("add eax,ecx"); // eax ← eax + ecx.
} // eax には 被演算子1+被演算子2がセットされる
となる。ここで code(str) は文字列 str をコードとして出力する関数である。
たくさんの演算子があるが、各演算子が構文規則に従って、
それぞれの役割分担を果たすだけでよい。
次に、制御文の例として、つぎのような while文を考える。
while (<条件式>) <文> ; // WhileStmt ::= "while" "(" Exp ")" Stmt
これは、<条件式>で表わされる条件が成り立つ間、<文>を繰り返し実行する。
while文は次に示すように、ラベルを含んだコードを生成する。
void while() {
code("L1:");
expr(); // 条件式のコード生成。結果は eax にセットされる。
code("jz L2"); // eax の値が 0 のとき L2 へジャンプ
stmt(); // 文のコード生成
code("jmp L1"); // 無条件に L1 へジャンプ
code("L2:"); // while文を抜けて、次の文へ
}
制作演習のCコンパイラでは、下に示す Name構造体で関数や変数を管理する。 名前管理表は大きくはグローバル名前管理表とローカル名前管理表からなるが、 Name構造体配列は Names[NMSIZE] の一つで、 Names[0] から Names[nGlobal-1] までがグローバル名前管理表で、 Names[nGlobal] から Names[nLocal-1] までがローカル名前管理表となる。
グローバル変数、関数(の名前やアドレス)、構造体定義はグローバル名前管理表に登録する。 これらの登録時にはローカル変数表は存在しない。
関数定義の処理に入ると、その時点でローカル名前管理表が誕生する。 最初に関数の仮引数が登録される。
関数本体(ブロック)の処理に入ると、引き続いて新たなローカル名前管理表が作成される。 前のローカル名前管理表との境界はブロック処理を担当する CompoundStatement関数のローカル変数にスタート時のnLocalの値記憶しておき、 そのブロック処理が終わった段階で、 nLocalの値を元の値に戻すことにより、ローカル名前管理表の解放となる。
関数定義が終わった場合は、ローカル名前管理表は皆無となり、 新たな関数名やグローバル変数はグローバル名前管理表に登録される。 つまり、nLocalは大きくなったり小さくなったりするが、nGlobalは一方的に大きくなるだけで、 小さくなることはない。 関数情報はJITコンパイラの前処理でも使用するため、グローバル名前管理表は最後まで廃棄することはない。
変数の探索は最初にローカル名前管理表に対して行う。 末尾から探索するため、境界が分からなくても、まず自ブロック、次に親ブロック、 更にその親を探索することになる。
searchName0関数は、見つかった場合はNames配列の添え字を返す。 見つからなかった場合には -1 を返す。
searchName関数は内部的にはsearchName0関数を使い、 見つかった場合はそのエントリのポインタを返す。 見つからなかった場合は、ローカル名前管理表の探索では NULL を返す。 グローバル名前管理表の探索では コンパイルしているプログラムに文法エラーがあることから、 エラーメッセージを表示して終了する。
終了させてはいけないときは、searchName0関数を使う。
//--------------------------------------------------------------------------------------//
// 名前管理表 //
//--------------------------------------------------------------------------------------//
#define NMSIZE 20000 // 名前管理表のサイズ
enum { GLOBAL = 0, LOCAL };
enum { NM_VAR = 1, NM_FUNC, NM_STRT, NM_MEMB }; // 名前の種別
typedef struct {
int type; // 名前の種別
int dataType; // データ型
char *name; // 変数名または関数名
int address; // 相対アドレス
int size[8]; // 配列サイズ
int ptrs; // []の数(配列次元数)+ *(ポインタ)の個数
} Name;
Name Names[NMSIZE]; // 名前管理表.
int nGlobal, nLocal; // 次の位置、現在の登録数 nGlobal, nLocal-nGlobal
// 指定された名前表から指定された名前を探す
int searchName0(int nB, int type, char *name) {
int n;
int nBgn = nB==GLOBAL ? 0 : nGlobal;
int nLast = nB==GLOBAL ? nGlobal : nLocal;
for (n = nLast; --n >= nBgn; ) {
if (strcmp(Names[n].name,name)==0 && Names[n].type==type) return n;
}
return -1; // 見つからなかった。
}
// 関数または変数情報を名前管理表に登録する
Name *appendName(int nB, int type, char *dt, char *name, int addr) {
Name nm = { type, NMSIZE + *dt, name, addr };
Name *pNew = nB==GLOBAL ? &Names[nGlobal++] : &Names[nLocal++];
*pNew = nm; // memcpy(pNew, &nm, sizeof(Name)) と等価
return pNew; // 新しいエントリのアドレスを返す
}
Name *searchName(int nB, int type, char *name) {
int n = searchName0(nB, type, name);
if (n >= 0) return &Names[n];
if (nB == GLOBAL) error("searchName: '%s' undeclared", name);
return NULL;
}