コンパイル過程上の第2のフェーズである構文解析について説明する。 構文解析の方法は、大きくは下向き(top-down)解析法と上向き(bottom-up)解析法に分類される。
下向き(top-down)構文解析法は構文解析木の根から始めて下に向かう。 構文規則に素直に対応した解析法である。
再帰的下向き解析法(再帰降下法)は、構文規則上の各非終端記号について、 ひとつずつ再帰的な処理を対応させ、この手続きの集まりによって構文解析を行う。 解析プログラムは構文規則を書き下したものとなる。
演算子が*と+の構文規則は下(構文規則 A)のように表した場合、 それ自身を再び左から使って定義されている(左再帰的)。 これをそのままプログラム化すると、解析が無限ループに陥る。
構文規則 A. <式> ::= <式> + <項> | <項> <項> ::= <項> * <変数> | <変数>
次のような等価な構文規則に置き換えることにより、 無限ループの問題が回避できる。 ここで、{ X } は X が 0 個以上並んだものを表す。
構文規則 B.
<式> ::= <項>{ + <項> } ・・・ (1)
<項> ::= <変数> { * <変数> } ・・・ (2)
<変数> ::= a | b | c ・・・ (3)
ここでは、参考までに構文規則 A. を示した。 規則 A. から規則 B. に変換するのではなく、最初から、規則 B. を考える方がいい。
例えば、
B * C + D / Eの場合、*、/ が +、- より優先順位が高いから B*C および D/E をひと塊として、
(B*C) +
(D/E) のように捉える。
トップダウン的には <式> ::= <項> + <項> となる。
*、/ はあったとしても、+、− がないようなケースは <式> ::= <項> と書く。
+が二つの場合、<式> ::= <項> + <項> + <項> となる。
+の数は0個以上任意の数になるため、規則 B. の (1) のように書く。
構文規則は演算子の優先順位が低い順に書く。 このことから (2) は簡単に理解できる。+と*は共に2項演算のために、全く同じ形となる。
*よりも更に優先順位が高い <変数> は二項演算ではないため、書き方は変わる。
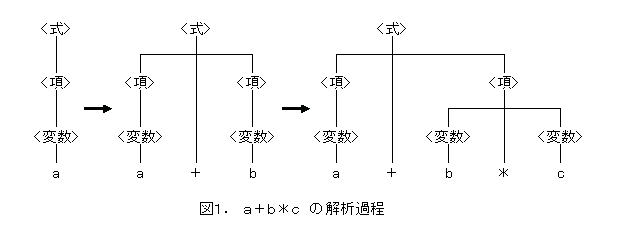
a + b * c の解析過程を説明する。 上の構文規則は演算子 * は演算子 + よりも優先順位が高いことを表している。

通常のコンパイラでは、この解析過程でツリー構造のデータ(構文解析木) を生成し、構文解析以降のフェーズである意味解析、コード生成で使用する。 プログラミング言語の仕様が限定的な場合、上述の構文解析のフェーズで、 併行して、意味解析、コード生成を行うことができるので、 ツリー構造のデータ生成は必須ではない。
構文解析木を、末端の葉に対応する入力トークン列から始まって、次々と上向きに 木の根の方に向かって作っていく方法が上向き(bottom-up)構文解析法である。 構文規則で言えば、右辺の記号列を左辺で置き換えながら(還元しながら)、 開始の非終端記号へと向かって処理をしていく。 以下、上向き構文解析法のひとつである演算子順位文法について説明する。
A ::= … B C …A, B, C は非終端記号。
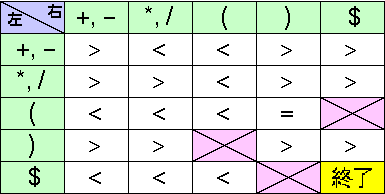
<, >, = のうちたかだか1個の関係しか成り立たない。
::= ( <式> ) ・・・
( と ) の優先順位は同じ。
即ち ( = )
例: <式> ::= <式> + <項> <項> ::= <因子> * <項>この場合 + < *
例: <因子> ::= ( <式> ) <式> ::= <式> + <項>このとき + > )
・ a = b : A → …ab… または A → …aBb…
・ a < b : B → …aA…という生成規則が存在し,A → b… または A → Cb…
・ a > b : B → …Ab…という生成規則が存在し,A → …a または A → …aC
ただし,小文字は終端記号,大文字は非終端記号
・式を$と$で囲む。$ の順位も必要。 ・本来は「数字」「識別子」にも順位は存在 (後で述べるアルゴリズムでは不要)
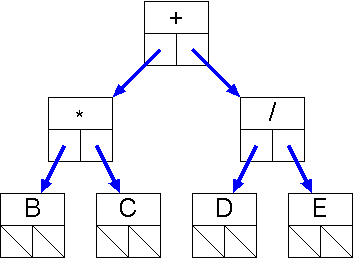 |
B * C + D / E 四つ組による表現 (*, B, C, T1) (/, D, E, T2) (+, T1, T2, T3) |
|---|
演算子順位法はシンプルだが、一般的な言語の構文解析には向かない。
LR法は入力を左から右へ走査し、最右の規則を導く。 LR構文解析は入力とスタック、構文解析表からなる。
構文解析表の作り方はここでは省略する。 例えば 参考文献[3]に述べられている。
入力は1記号ずつ左から右に読む。スタックには、
s0 X1 s1 X2 s2 X3 s3.... Xm smという記号列を積む。sは状態に対応した記号である。 Xは文法記号で、実際は必要ないが説明のために加えてある。 構文解析表は構文解析動作関数ACTION と行き先関数GOTOの2つの部分からなる。 LR構文解析のプログラムは現在のスタックの最上段の状態smと入力記号aiをもちいて、 ACTION[sm, ai]を引いて、以下の動作のどれかをとる。
数式の文法
(1) Expr → Expr '+' Term
(2) Expr → Term
(3) Term → Term '*' Factor
(4) Term → Factor
(5) Factor → '(' Expr ')'
(6) Factor → identifier
の構文解析表は次のようになる。
a * b + c とか (2 + 3)*4 はこの文法を満たしている。
SLR(simple LR)法では、文法より、次のような構文解析表を作り、 それを用いたオートマトンで構文解析をする。
| ACTION | GOTO (非終端記号) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| state | id | + | * | ( | ) | $ | E | T | F |
| 0 | s5 | s4 | 1 | 2 | 3 | ||||
| 1 | s6 | acc | |||||||
| 2 | r2 | s7 | r2 | r2 | |||||
| 3 | r4 | r4 | r4 | r4 | |||||
| 4 | s5 | s4 | 8 | 2 | 3 | ||||
| 5 | r6 | r6 | r6 | r6 | |||||
| 6 | s5 | s4 | 9 | 3 | |||||
| 7 | s5 | s4 | 10 | ||||||
| 8 | s6 | s11 | |||||||
| 9 | r1 | s7 | r1 | r1 | |||||
| 10 | r3 | r3 | r3 | r3 | |||||
| 11 | r5 | r5 | r5 | r5 | |||||
C言語による構文解析プログラムを以下に示す。実行結果を下の右に示す。
|
( 1) input=id state= 0 action= 5: shift push( 5) ( 2) input= * state= 5 action=-6: reduce LR[0][8] push( 3) ( 3) input= * state= 3 action=-4: reduce LR[0][7] push( 2) ( 4) input= * state= 2 action= 7: shift push( 7) ( 5) input=id state= 7 action= 5: shift push( 5) ( 6) input= + state= 5 action=-6: reduce LR[7][8] push(10) ( 7) input= + state=10 action=-3: reduce LR[0][7] push( 2) ( 8) input= + state= 2 action=-2: reduce LR[0][6] push( 1) ( 9) input= + state= 1 action= 6: shift push( 6) (10) input=id state= 6 action= 5: shift push( 5) (11) input= $ state= 5 action=-6: reduce LR[6][8] push( 3) (12) input= $ state= 3 action=-4: reduce LR[6][7] push( 9) (13) input= $ state= 9 action=-1: reduce LR[0][6] push( 1) (14) input= $ state= 1 action=9999: 受理! |
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define x 9998
#define A 9999 // 受理
char *token[] = { "id", "+", "*", "(", ")", "$" };
int LR[][] = {
// 0 1 2 3 4 5 6 7 8
// id + * ( ) $ E T F
{ 5, x, x, 4, x, x, 1, 2, 3 }, // 0
{ x, 6, x, x, x, A, x, x, x }, // 1
{ x,-2, 7, x,-2,-2, x, x, x }, // 2
{ x,-4,-4, x,-4,-4, x, x, x }, // 3
{ 5, x, x, 4, x, x, 8, 2, 3 }, // 4
{ x,-6,-6, x,-6,-6, x, x, x }, // 5
{ 5, x, x, 4, x, x, x, 9, 3 }, // 6
{ 5, x, x, 4, x, x, x, x,10 }, // 7
{ x, 6, x, x,11, x, x, x, x }, // 8
{ x,-1, 7, x,-1,-1, x, x, x }, // 9
{ x,-3,-3, x,-3,-3, x, x, x }, // 10
{ x,-5,-5, x,-5,-5, x, x, x }, // 11
};
int r2n[] = { 6, 6, 7, 7, 8, 8 }; // rule番号→LR表の列番号
int pops[] = { 3, 1, 3, 1, 3, 1 };
int stack[100];
int sp = 0;
void push(int s) { stack[sp++] = s; }
int peek() { return sp > 0 ? stack[sp-1] : x; }
int pop() { return sp > 0 ? stack[--sp] : x; }
int tokenNumber(char *str) {
int n;
for (n = 1; n < sizeof(token)/sizeof(char*); n++)
if (strcmp(str, token[n]) == 0) return n;
return 0; // identifier or number
}
void main() {
//char *input[] = { "(", "2", "+", "3", ")", "*", "5", "$" };
char *input[] = { "a", "*", "b", "+", "c", "$" };
int ix, c, n, step, state, action;
ix = 0;
c = tokenNumber(input[ix++]);
push(0); // 初期状態をプッシュ
for (step = 1;;step++) {
state = peek();
action = LR[state][c];
printf("(%2d) input=%2s state=%2d action=%2d: ",
step, token[c], state, action);
if (action == x) {
exit(1); // エラー終了
} else if (action == A) {
printf("受理!\n");
exit(0);
} else if (action >= 0) { // shift: 次の状態をスタックに積む
push(action);
printf("shift %9s push(%2d)\n", "", action);
c = tokenNumber(input[ix++]);
} else { // action < 0 // reduce:
for (n = pops[-action-1]; n-- > 0; ) pop();
state = LR[peek()][r2n[-action-1]];
printf("reduce LR[%d][%d] push(%2d)\n",
peek(), r2n[-action-1], state);
push(state);
}
}
}