トップ ＞ デジタル回路 ＞ エンコーダとデコーダ

エンコーダとデコーダ

１．エンコーダとデコーダ

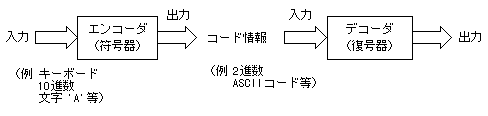
下にエンコーダとデコーダの概念図を示す。

エンコーダとは、例えばキーボードの 'Ａ' というアルファベット を、計算機内部で使用するアスキーコード（ASCII）に変換する装置のことを指す。一般には、人間が直接識別したりする 情報を、計算器が扱いやすい情報（符号）に変換するための装置（符号器）である。 一方、デコーダはこのエンコーダの逆の操作をする装置である。

２．8入力3出力エンコーダ

エンコーダの例として、 10(8)進数を2進数に変換する回路を取り上げる。 ここでは、8入力（Z7,Z6,Z5,...,Z0）のいずれか 1つが 値 1をとるものとして、それらの2進数に対応する3ビットの 出力（A2,A1,A0）を生成する回路を考える。

はじめに、真理値表を作成する。

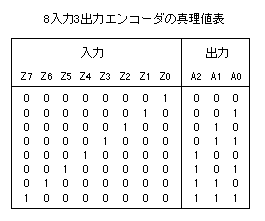
次に、この真理値表から出力（A2,A1,A0）の各々を、 8つの入力（Z7,Z6,Z5,...,Z0）を用いて表す。

上の論理式は、これ以上簡略化することはできない。 これらの式をMIL記号を用いて表現すると、次に示す回路図が得られる。
[Reference: http://laputa.cs.shinshu-u.ac.jp/~yizawa/logic/chap8/chap8.html]

３．デコーダ

デコーダの例として、 4ビットの2進数を10進数に変換する回路を取り上げる。

すなわち、入力（A,B,C,D）を2進数(Aが最上位でDが最下位ビット) について、その10進数に 対応する10個の出力（Z0,Z1,Z2,...,Z9）を出力する回路を考える。

はじめに、真理値表を作成する。

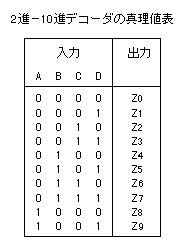
次に、この真理値表から出力（Z0,Z1,Z2,...,Z9）の各々を A,B,C,Dを用いて表す。
　　　Z0 = A・B・C・D
　　　Z1 = A・B・C・D
　　　Z2 = A・B・C・D
　　　　　・・・
　　　Z9 = A・B・C・D
これを素直に４入力ANDゲートを用いて表現すると、下の回路となる。

A,B,C,Dの横の数字をクリックすると値が変わります

上の回路では、10以上の数値を指定すると出力（Z0,Z1,Z2,...,Z9）は 全て０となる。

このとき、4ビットの入力（A,B,C,D） について、10進数の10〜15までの組合せが使用されていない ことを利用すると、論理式はさらに簡略化できる。

カルノー図法による論理式の簡単化は別のページにまとめているのでここでは省略する。 但し、演習ページでは、A,B,C,Dの並びがこのページとは真逆になっている。

その結果を以下に示す。

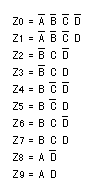
これらをMIL記号を用いて表現すると、以下に示すデコーダの回路が得られる。10進数の10〜15までは使用禁止のため、 入力（A,B,C,D）の値が10以上のとき、出力の値が正しくならない ことに注意がいる。


[Reference: http://laputa.cs.shinshu-u.ac.jp/~yizawa/logic/chap8/chap8.html]

４．文字表示回路

液晶のディジタル時計等には、下の図のような7つのセグメントからなる表示器が使用されている。

4ビットの入力（A,B,C,D）を入力すると、この2進数に対応する 10進数（0〜9）の数字が表示される。

この回路の真理値表は以下のようになる。


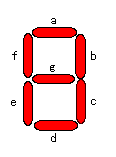　７セグメント表示器

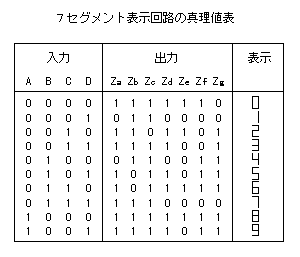
これらの出力について論理式を作成し、これを簡略化すると次の式が得られる。

カルノー図法による論理式の簡単化は別のページにまとめているのでここでは省略する。 但し、演習ページでは、A,B,C,Dの並びがこのページとは真逆になっている。

これらの論理式から、以下に示す文字表示回路が得られる。


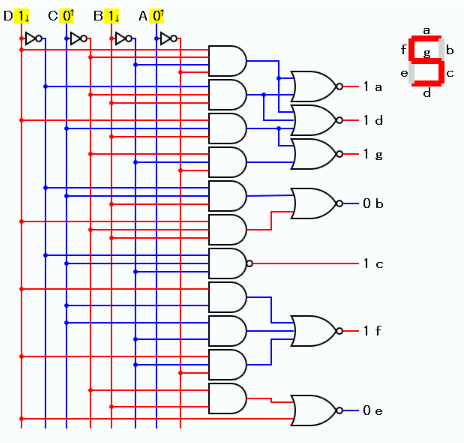
この場合も、10進数の10〜15までは使用禁止のため、 入力（A,B,C,D）の値が10以上のとき、出力値が正しくならない。

JavaScriptによるシミュレーションを下に示す。 （A,B,C,Dの横の数字をクリックすると値が変わります。）