トップ ＞ デジタル回路 ＞ 同期式カウンタ―Dフリップフロップ使用（２）

同期式カウンタ―Dフリップフロップ使用（２）

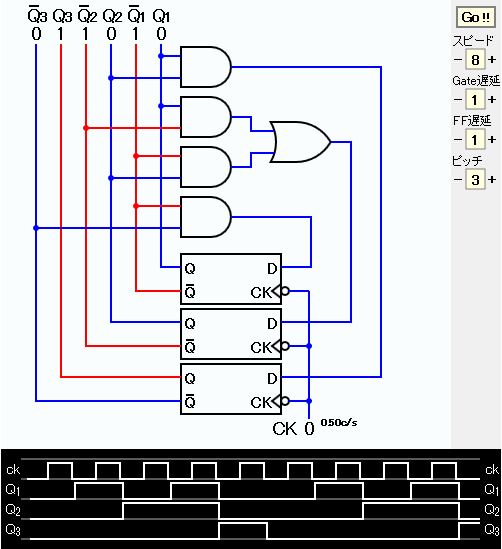
前のページでは、なるべく少ない部品で回路を構成することを考えた。 回路が複雑になると、分かりにくくなる。 このページではフリップフロップの周辺はANDゲートとORゲートで構成し、フリップフロップは縦に並べて、 画一的な構成にする。

１．同期式５進カウンタ

Dフリップフロップによる同期式５進カウンタは前のページで取り上げたが、 ここでは、回路図の書き方を変える。 まず、真理値表は前にも示したが、次のようになる。

Dフリップフロップを使った５進カウンタの真理値表
Q1Q2Q3 D1D2D3
000 100
100 010
010 110
110 001
001 000
101 xxx
011 xxx
111 xxx

この真理値表から加法標準形を使って論理式を表し、簡単化すると 

　D1 ＝ Q1・Q3
　D2 ＝ Q1・Q2＋Q1・Q2
　D3 ＝ Q1・Q2
となる。前のページではD2の論理式はXORで表したが、今回はANDゲートとORゲートのみ、XORは使用しないため、上のような表現にとどめる。 また、前回はカット・アンド・トライ法（試行錯誤法）で、論理式の簡単化を行ったが、当然、カルノー図法を使うことができる。

カルノー図法による簡単化は別のページで 演習問題としているのでここでは省略する。

シミュレーションのスナップを下に示す。 回路図の表現方法が変わっただけであるから、タイムチャートは同じである。 前の回路よりも調和がとれていて見やすいであろう。

JavaScriptによるシミュレーションを下に示す。

２．同期式６進カウンタ

Dフリップフロップによる同期式６進カウンタを設計する。 まず、真理値表は次のようになる。

Dフリップフロップを使った６進カウンタの真理値表
Q1Q2Q3 D1D2D3
000 100
100 010
010 110
110 001
001 101
101 000
011 xxx
111 xxx

この真理値表から加法標準形を使って論理式を表し、簡単化すると 

　D1＝Q1
　D2＝Q1・Q2＋Q1・Q2・Q3
　D3＝Q1・Q3＋Q1・Q2
となる。

カルノー図法による簡単化は別のページで 演習問題としているのでここでは省略する。

シミュレーションのスナップショットを下に示す。 論理式はANDゲートとORゲートで構成すると、秩序のある回路図となるので見やすい。 タイムチャートからこのカウンタの出力が０、１、２、３、４、５、０、１、… となっていることが確認できる。

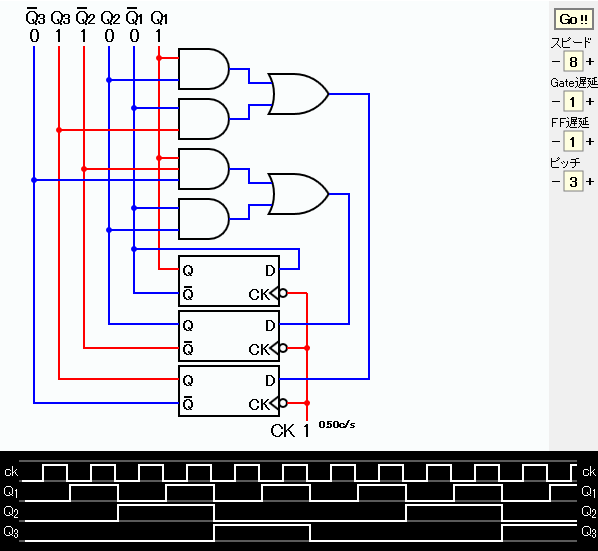
この図の元となるJavaScriptのシミュレーションを下に示す。

３．同期式７進カウンタ

Dフリップフロップによる同期式７進カウンタを設計する。 まず、真理値表は次のようになる。

Dフリップフロップを使った７進カウンタの真理値表
Q1Q2Q3 D1D2D3
000 100
100 010
010 110
110 001
001 101
101 011
011 000
111 xxx

この真理値表から加法標準形を使って論理式を表し、簡単化すると 

　D1＝Q1・Q2＋Q1・Q3
　D2＝Q1・Q2＋Q1・Q2・Q3
　D3＝Q2・Q3＋Q1・Q2・Q3
となる。一行目は単独では 　D1＝Q1・(Q2＋Q3) とした方法が回路が簡単となるが、ここでは、括らない。

カルノー図法による簡単化は別のページで 演習問題としているのでここでは省略する。

シミュレーションのスナップショットを下に示す。 論理式はANDゲートとORゲートで構成すると、秩序のある回路図となるので見やすい。 タイムチャートからこのカウンタの出力が０、１、２、３、４、５、６、０、１、… となっていることが確認できる。

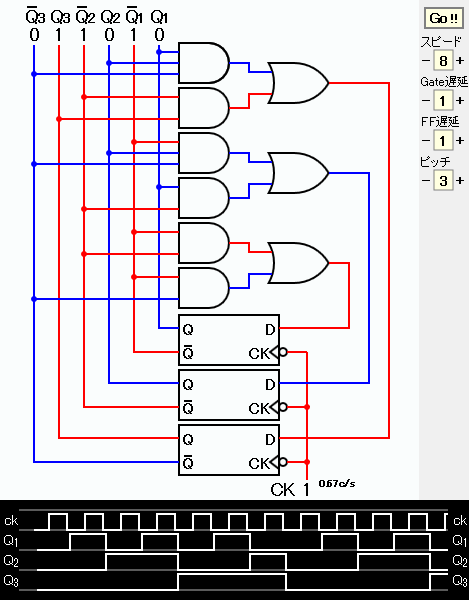
この図の元となるJavaScriptのシミュレーションを下に示す。

４．同期式８進カウンタ

この方法では２のN乗で表される８進の場合でも、回路は簡単にはならない。

Dフリップフロップによる同期式８進カウンタを設計する。 まず、真理値表は次のようになる。

Dフリップフロップを使った７進カウンタの真理値表
Q1Q2Q3 D1D2D3
000 100
100 010
010 110
110 001
001 101
101 011
011 111
111 000

この真理値表から加法標準形を使って論理式を表し、簡単化すると 

　D1＝Q1
　D2＝Q1・Q2＋Q1・Q2
　D3＝Q1・Q3＋Q2・Q3＋Q1・Q2・Q3
となる。二行目はXORゲートで表現できるが、ここではXORを使わない。

カルノー図法による簡単化は別のページで 演習問題としているのでここでは省略する。

シミュレーションのスナップを下に示す。 タイムチャートからこのカウンタの出力が０、１、２、３、４、５、６、７、０、１、… となっていることが確認できる。

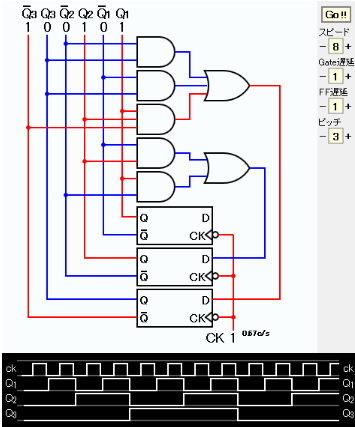
この図の元となるJavaScriptのシミュレーションを下に示す。

５．同期式９進カウンタ

Dフリップフロップによる同期式９進カウンタを設計する。 まず、真理値表は次のようになる。

Dフリップフロップを使った９進カウンタの真理値表
Q1Q2Q3Q4 D1D2D3D4
0000 1000
1000 0100
0100 1100
1100 0010
0010 1010
1010 0110
0110 1110
1110 0001
0001 0000
1001 xxxx
0101 xxxx
1101 xxxx
0011 xxxx
1011 xxxx
0111 xxxx
1111 xxxx

この真理値表から加法標準形を使って論理式を表し、簡単化すると 

　D1＝Q1・Q4
　D2＝Q1・Q2＋Q1・Q2
　D3＝Q1・Q3＋Q2・Q3＋Q1・Q2・Q3
　D4＝Q1・Q2・Q3
となる。

カルノー図法による簡単化は別のページで 演習問題としているのでここでは省略する。

前にも述べたが、この構成では、XORゲートを使ったり、 共通因子があっても、かっこで括ったりしない。上の論理式をAND、ORゲートで実現する。

シミュレーション実行のハードコピーを下に示す。 タイムチャートからこのカウンタの出力が０、１、２、３、４、５、６、７、８、０、１、… となっていることが確認できる。

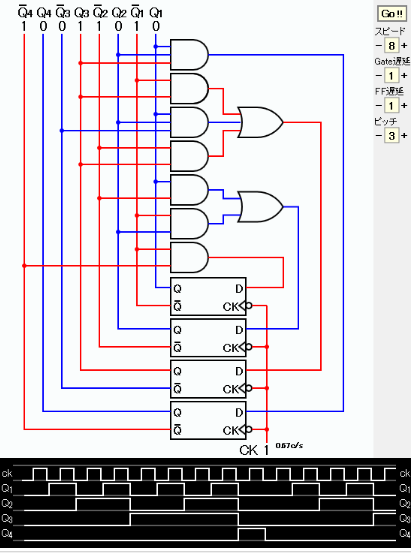
この図の元となるJavaScriptのシミュレーションを下に示す。

６．同期式１０進カウンタ

Dフリップフロップによる同期式１０進カウンタを設計する。 まず、真理値表は次のようになる。

Dフリップフロップを使った１０進カウンタの真理値表
Q1Q2Q3Q4 D1D2D3D4
0000 1000
1000 0100
0100 1100
1100 0010
0010 1010
1010 0110
0110 1110
1110 0001
0001 1001
1001 0000
0101 xxxx
1101 xxxx
0011 xxxx
1011 xxxx
0111 xxxx
1111 xxxx

この真理値表から加法標準形を使って論理式を表し、簡単化すると 

　D1＝Q1
　D2＝Q1・Q2＋Q1・Q2・Q4
　D3＝Q1・Q3＋Q2・Q3＋Q1・Q2・Q3
　D4＝Q1・Q4＋Q1・Q2・Q3
となる。

カルノー図法による簡単化は別のページで 演習問題としているのでここでは省略する。

シミュレーション実行のハードコピーを下に示す。 タイムチャートからこのカウンタの出力が０、１、２、３、４、５、６、７、８、９、０、１、… となっていることが確認できる。

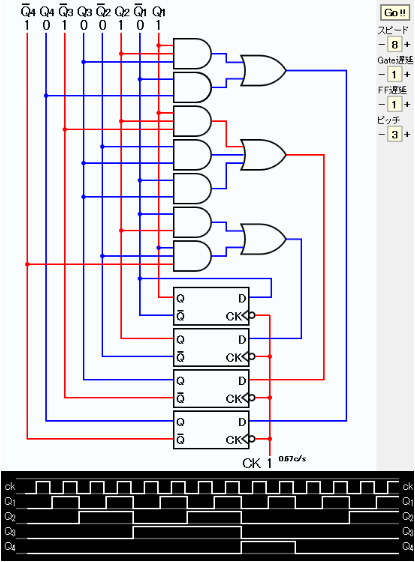
この図の元となるJavaScriptのシミュレーションを下に示す。

７．同期式１１進カウンタ

Dフリップフロップによる同期式１１進カウンタを設計する。 まず、真理値表は次のようになる。

Dフリップフロップを使った１１進カウンタの真理値表
Q1Q2Q3Q4 D1D2D3D4
0000 1000
1000 0100
0100 1100
1100 0010
0010 1010
1010 0110
0110 1110
1110 0001
0001 1001
1001 0101
0101 0000
1101 xxxx
0011 xxxx
1011 xxxx
0111 xxxx
1111 xxxx

この真理値表から加法標準形を使って論理式を表し、簡単化すると 

　D1＝Q1・Q2＋Q1・Q4
　D2＝Q1・Q2＋Q1・Q2・Q4
　D3＝Q1・Q3＋Q2・Q3＋Q1・Q2・Q3
　D4＝Q2・Q4＋Q1・Q2・Q3
となる。

カルノー図法による簡単化は別のページで 演習問題としているのでここでは省略する。

シミュレーション実行のハードコピーを下に示す。 タイムチャートからこのカウンタの出力が０、１、２、３、４、５、６、７、８、９、１０、０、１、… となっていることが確認できる。

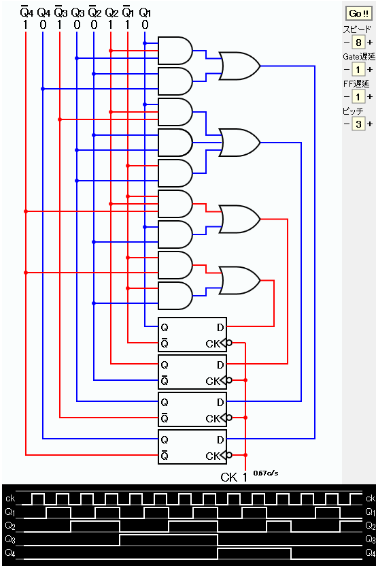
この図の元となるJavaScriptのシミュレーションを下に示す。