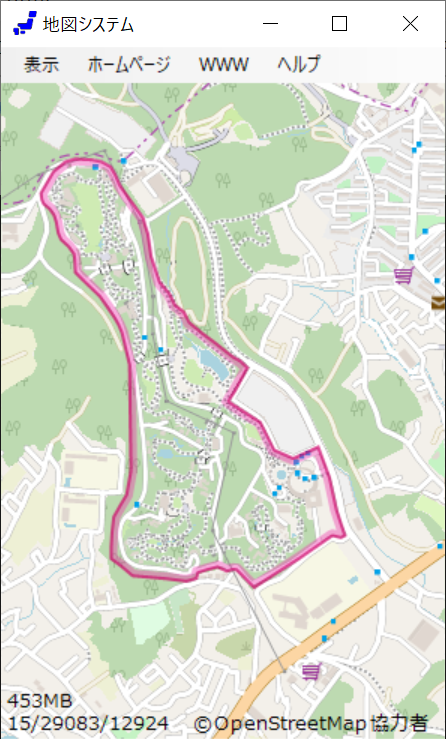
標準OSMでは、テーマパークや動物園の境界線は下に示すように、ラインの垂直方向に gradation のかかった線(色違いの二重線)を引く。 外側を濃く、内側を薄くした線を描画している。
C# の場合には、このような線を比較的簡単に描画する機能を備えている。 一方、Java とか Android Java にはこのような機能が見当たらない。
PC地図システム自体は C# で開発しているが、 本命は Android Java によるスマホ用地図アプリである。 C# と Android Java で共通的に使えるプログラムを目指している。 このため、記事[1] に記載した方法は敢えて使用せず、 自前プログラムでこのような二重線を描画する。
スマホ用初代の地図アプリでは、すでに、自前プログラムでこのような二重線を描画している。 今回、そのプログラムをリファインした。
原理的には境界線の少し内側に相似的な閉曲線を描くことになる。 単純に座標値に 0.99 を掛ければ１％小さくなるならばたやすい話であるが、 そんな簡単な話ではない。
線分単位で、境界線の内側に平行線を描くことは比較的に簡単である。 しかし、それでは線分同士がノード付近で交差したり、繋がらなかったりする。
平行な線分同士で交点を求めてその交点の座標値を新しいノードの座標値とすればよい。
下のプログラムで、 p0、p1、p2、... は元の多角形の頂点座標である。 p0-p1、p1-p2、… といった線分に対して平行な線分(垂直方向に dy だけ離れている) b0-e0、b1-e1、… を考え、その交点を新しい座標値とする。
PointF[] Convert(PointF[] points, float dy) {
PointF[] dst = new PointF[points.Length];
PointF b0=new PointF(), e0=new PointF();
PointF b1=new PointF(), e1=new PointF();
PointF sb1=new PointF(), se1=new PointF(); // 平行線分の端点座標
PointF p0 = points[0];
for (int n = 1; n < points.Length; n++) {
PointF p1 = points[n];
double angle = getRadian(p0, p1); // ラジアン
b1.X = (float)(p0.X - dy * Math.Sin(angle));
b1.Y = (float)(p0.Y + dy * Math.Cos(angle));
e1.X = p1.X + (b1.X - p0.X); // 線分 p0-p1 に平行な
e1.Y = p1.Y + (b1.Y - p0.Y); // 線分 b1-e1
if (n == 1) {
dst[0] = b1; // polygon の場合は後で書き換えがおきる
sb1 = b1; // 最後に使う
se1 = e1;
} else {
dst[n-1] = getIntersection(b0, e0, b1, e1);
}
p0 = p1;
b0 = b1;
e0 = e1;
}
if (type == 1) {
dst[dst.Length-1] = e1;
} else {
dst[0] = dst[dst.Length-1] = getIntersection(b0, e0, sb1, se1);
}
return dst;
}
// 線分と線分の交点座標を求める
PointF getIntersection(PointF p0, PointF p1, PointF p2, PointF p3) {
float S1 = ((p3.X - p2.X) * (p0.Y - p2.Y) - (p3.Y - p2.Y) * (p0.X - p2.X)) / 2;
float S2 = ((p3.X - p2.X) * (p2.Y - p1.Y) - (p3.Y - p2.Y) * (p2.X - p1.X)) / 2;
float X = p0.X + (p1.X - p0.X) * S1 / (S1 + S2);
float Y = p0.Y + (p1.Y - p0.Y) * S1 / (S1 + S2);
return new PointF(X, Y);
}
// 単位：ラジアン
double getRadian(PointF p, PointF q) {
return Math.Atan2(q.Y - p.Y, q.X - p.X);
}
このプログラムの実行結果が上に示した図であるが、 交点座標算出で S1 + S2 の値が 0 になることはないか、まだ、十分に吟味はしていない。
また、このプログラムは多角形(polygon)の二重境界線描画に使うだけでなく、 土手や崖などのレンダリングにも使う予定であるが、その確認はまだ行っていない。
線分p0-p1 と線分p2-p3 が平行な場合、交点は存在しない。 上のプログラムでは S1+S2 が 0 になるものと思われる。 しかし、この場合は元々 p1 と p2 は同じ点であり、折れ線を切り離して、それぞれ平行移動したものであるから、 線分を無限の長さの直線とすれば、必ず交点は存在する。
頂点が重なっていた場合、線分にはならないため、まず、getRadian で角度を求めることができない。
元の OSMデータに頂点の重なりエラーが存在するケースと、極めて接近していたため、丸め誤差により、 頂点座標が一致するケースがありうる。
低、中ズーム用データはノードを間引いているため、頂点座標の重なりは排除されるが、 高ズーム用データでは間引きを行っていないため、頂点の重なりが起こる可能性が残っている。
頂点の重なり排除はこのプログラム PointF[] Convert(PointF[] points, float dy)で行うのではなく、 引数 PointF[] points の作成元で行うべきであろう。
単なるライン描画やポリゴン塗りつぶしでは頂点座標の重なりがあってもエラーにならないであろうが、 処理の無駄がある。
OSMデータの元々の座標は極座標である。それを世界XY平面座標に変換するところでも丸め誤差があるが、 最終的には空間検索結果をタイル相対座標に変換したものが PointF[] points である。 頂点の重なり排除はここで行うのがベストであろう。
相対座標値の単位は画素である。レンダリング上の座標値の単位と同じである。 頂点間の距離が 0.1画素もないような線分は実際上描画できない(目に見えない)。
当面、座標値列データの先頭と末尾を除いて、中間にあるノードは その前のノードとの距離が 0.1画素未満の場合は無視する。 正確にユークリッド距離を求めるまでもないので、X軸、Y軸方向の距離が共に 0.1画素未満のノードを無視することにする。 0.1 という数値は、もっと大きくしてもよい。
0.5にしてみたが、主に１、２ノードの間引きが起きるだけであった。 ただし、36ノードから27ノードになったケースもある。