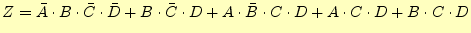カルノー図法

１．カルノー図

カルノー図法は、表を使って、論理式を簡単化する。 例として論理式

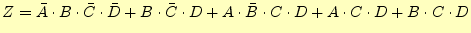　　（１）

カルノー図のための表をまず作成する。 論理変数が4個なので、図1の表を作成する。

図 1: カルノー図を作成するための表(4変数)。

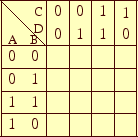
この表の縦および横は、それぞれの論理変数の値を示す。 ただし、真理値表と論理変数の並びが異なる。 真理値表は、2進数で値の小さい順に並んでいた。 しかし、カルノー図は、グレイコードで並んでいる。 上下の行(および左右の列)を比較すると、常に１ビットしか異なっていない。 上の端のセルと下の端のセル、右端のセルと左端のセルは連続していると考える。

表の枠が出来たならば、その中に論理変数に応じた論理式の値を入れていく。 今回の式の右辺は、5個の項から出来ている。 その5個の項のうち、どれかが1になった場合、論理式の値が1になる。

論理式が1になる論理変数（A, B, C, D）の値を探す。今後、論理変数の値はこの並びとする。

右辺第1項の値が1になるのは、（0, 1, 0, 0）の場合のみである。 そこで、それに対応するセル2行1列に1を書き込む。

右辺第2項の場合、A の項が無いのでそれは0でも1でも良く、（0, 1, 0, 1） と（1, 1, 0, 1）のとき 論理式の値が1になる。これも、表に1を書き込む。

同様に右辺第3項は、（1,0,1,1）第4項は（1,0,1,1）と（1,1,1,1） 、 第5項は（0,1,1,1）と（1,1,1,1）のとき論理式の値が1となる。 それぞれ1を書き込む。

次に、この表の中の全ての1を出来るだけ数の少ない正方形を含む長方形(ループ)で囲みます。 ただし、囲む場合、次の条件に従う。

• 囲んだ長方形の中のセルは、全て1であること。 　
• 囲んだ長方形の中のセルの数は、1,2,4,8,... のように 2^Nであること。
• 同じセルを2つ以上のループで共有しても良い。
• カルノー図の上下の端、および左右の端は連続していると考える。

図 2: カルノー図の例

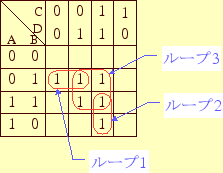
最後に、この3個のループから共通変数を取り出しその論理積を作る。 それぞれの論理積の論理和をとり、論理式を作る。 これが簡略化された論理式となる。 図2のループ1の共通変数の論理積は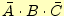である。 ループ2の場合は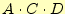 、 ループ3の場合はとなる。 これらの論理和は、

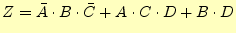
となる。これが、元の論理式を簡略化した結果である。

２．論理式の簡単化：カルノー図法

• カルノー図は、論理式や真理値表と同様に論理の表現法の一つ。
• 共通項で括るときに（A ＋ A）の形になる括り方を見つけやすい。
• 入力変数の数により枠の取り方が異なる。３変数と４変数の場合を下図に示す。

  
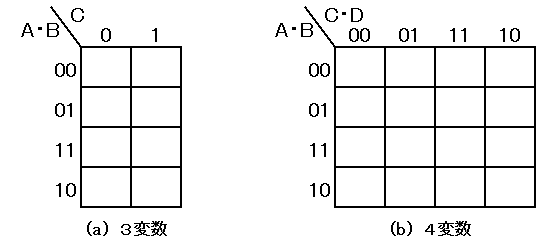
  　　　　　　　　図３.　カルノー図の枠の取り方

• 枠外の０や１は、行や列に割り当てられた変数の値を示す。
• 隣り合った枠の変数の値が一つだけ異なるようにするため、２進数とは違った順序となることに注意。 （このような順序のコードを グレイコードという）
• 下図は、各枠がどの変数の値の組合せになるかを３変数の例で示したものである。
  

  

• 書き込む出力の値は、普通１のみで、出力が０のときは空白とする。
• 真理値表から書き込むときは、入力変数の値が同じとなる枠に、出力の値を書き込む。
• 論理式は加法標準形から書き込み、ANDの形の各項に相当する枠に１を書き込む。 項の中の　の付く変数の値は０、 　の付かない変数の値は０と考える。
• 下図に、各枠がどの論理式に対応するかを３変数の例で示す。

  

３．カルノー図の使用例

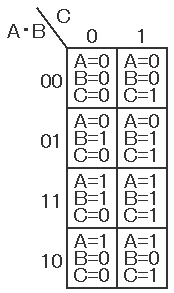
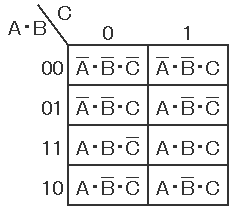
例１．下の左に示す真理値表をカルノー図にした結果をその右に示す。

1. いくつかの１をまとめて１つの項を作り出す。
2. 上下、左右の隣り合った領域をサークルとできる。 隣り合った枠は、どれか１つの変数の値が異なっているので、論理式に直した場合、 （A＋A）のような形ができて、値が異なっている変数を省略できる。
3. １の枠は全てサークルにとらねばならない。
4. サークルを構成する１の数は、2ⁿ個で、かつ最大数とする。 すなわち、1, 2, 4, 8, 16 のいずれかでなければならない。
5. ひとつの１を何回サークルにとってもよい。
6. 右端と左端の列は隣り合っているとする。 同様に、最上段の行と最下段の行は隣り合っているとする。

この例では４隅が一つのグループとなります。

例２．下の左に示す真理値表をカルノー図にした結果をその右に示す。

サークル�@は次のように考えます。

慣れれば、この計算が暗算で行えます。Aは０、Bは０と１、Cは１のセルに１があります。 Bは０と１があることから消します。残りはAが０、Cが１であることからA・Cとなります。 このように、目で追ってループの表す論理式を求めます。

【論理式を簡単化する場合】

次にあるような論理式を簡単化する場合、それぞれの項に対応したセルに１を書きます。 後は真理値表の場合と同じです。この例では出てきませんが、A、B、Cの３入力に対して たとえば A・Cのような項があれば、先ほどの式の変形とは逆に

A・C ＝ A・C （B＋B）

　　　＝ A・B・C＋A・B・C

と考えて、該当する二つのセルに１を書きこみます。

下に例を示しています。操作方法は真理値表の場合とほぼ同じです。

元の論理式の項をクリックすると、文字の色が赤に変わり、カルノー図の対応したセルの背景色が黄色に変わります。 （カルノー図のセルをクリックしても、この逆のことは起きません。）

４．練習問題

１．次の論理式をカルノー図法により簡単化しなさい。

２．次の論理式をカルノー図法により簡単化しなさい。

３．次の論理式をカルノー図法により簡単化しなさい。

４．次の論理式をカルノー図法により簡単化しなさい。

５．次の論理式をカルノー図法により簡単化しなさい。

６．次の論理式をカルノー図法により簡単化しなさい。

７．次の論理式をカルノー図法により簡単化しなさい。

実用上は加法標準形をマスターすれば、乗法標準形は使う必要がない。 双対関係にあることから、混乱する恐れもあるのでお勧めしない。 しかし、技法としては乗法標準形に対して直接、カルノー図を使うこともできる。 そのため、参考までに、その方法も載せる。

８．次の論理式をカルノー図法により簡単化しなさい。

５．練習問題

小テスト解説